Diseñar nuevos sistemas ópticos desde cero puede ser una tarea intimidante, especialmente si el sistema que intentamos crear es uno que debemos acertar antes de que se pueda construir algo, porque los componentes críticos simplemente aún no existen. Es simplemente una fantasía de nuestra imaginación, y de hecho es parte de nuestra tarea definirlo. Surgirán situaciones similares cuando exploremos diferentes diseños y queramos aprender cómo funcionan las cosas antes de emprender la tarea de construirlas realmente.
Imaginemos esto. Tienes que encontrar los requisitos para un sistema que nunca hemos estudiado antes y si hay un artículo científico que quizás esté relacionado con lo que necesitamos, ¿lo encontraremos? No es raro que reinventemos la rueda. Dirac reinventó el álgebra de Clifford cuando derivó las ecuaciones cuánticas para el electrón, así que obviamente, esto les sucede a los mejores. Así que supongamos que, decidas lo que decidas, la responsabilidad recae en nosotros.
La estrategia a seguir en este punto sería poner en marcha un modelo, una especie de mapa, pero no uno cualquiera: tiene que ser lo bastante detallado como para navegar por todos los recovecos esenciales (léase: grados de libertad), pero no tan intrincado como para que los árboles nos impidan ver el bosque. Aquí radica nuestro primer reto: a menos que esta máquina sea un primo cercano de algo que ya dominamos, nuestro mapa es más una conjetura que un evangelio. No sabemos qué caminos (grados de libertad) son los más importantes y cuáles son sólo detalles.
Sin la brújula adecuada (herramientas) para navegar por la complejidad, corremos el riesgo de simplificar en exceso nuestro mapa, limitados más por nuestra imaginación que por el terreno real.
Reducir la complejidad
Una forma de abordar esto, que he encontrado que funciona bien, es emplear una expansión matemática conocida alrededor del estado ideal del sistema que se está estudiando, esencialmente una expansión de Maclaurin. Dado que la herramienta que buscamos es una que libere nuestro análisis de nuestras propias limitaciones mentales, debe ser una que nos permita sondear nuestro sistema con un gran número de variables independientes.
Existen diferentes maneras de abordar esto, pero una que he encontrado que funciona muy bien es el llamado Muestreo del Hipercubo Latino (LHS), a veces también referido como un diseño que llena el espacio.
Generar un LHS lleva algo de tiempo, pero en la mayoría de los casos suele ser menos de unos pocos minutos, incluso si el número de variables independientes es grande. El tiempo para generar un LHS crece linealmente con el número de variables y a la 3ª potencia con el número de muestras. Afortunadamente, esta es solo una complejidad polinomial, o “fácil” si se pregunta a las personas de Complejidad Computacional.
Un ejemplo de dónde un gran número de grados de libertad (DOF) puede ser interesante es cuando queremos derivar la especificación para un sistema óptico, y los DOF son los coeficientes del polinomio de Zernike.
Lo que nos da la LHS es un conjunto de muestras distribuidas uniformemente en un espacio multidimensional, pero sigue dependiendo de nosotros hacer la pregunta correcta, y en este caso, prácticamente no hay preguntas incorrectas.
Entonces, por ejemplo, utilizando este conjunto de muestras, se pueden configurar simulaciones que exploren la varianza de una propiedad, o se puede simular cómo una propiedad determinista depende de nuestros grados de libertad. Ambas cosas pueden ser muy valiosas, pero antes de profundizar en ello, hablemos de cómo obtener algunos resultados para analizar.
Expansión de segundo orden
Por simple que parezca, se trata de un enfoque muy valioso que ofrece perspectivas que a menudo se convierten en momentos "ajá".
Del LHS, tenemos un conjunto de puntos y, utilizando estos puntos de muestreo en nuestro problema multidimensional, ejecutamos un número igual de simulaciones para obtener un resultado numérico para cada uno. Sin embargo, haber hecho todo eso no es muy esclarecedor. Necesitamos reducir esta complejidad. Necesitamos resumir todas estas simulaciones, que fácilmente podrían ser varios miles, en algo que podamos comprender, algo que, por así decirlo, separe el grano de la paja.
La forma de hacerlo es intentar expresar nuestros resultados mediante una expansión de segundo orden,
Esto es muy similar a la forma en que expresaríamos una expansión de MacLaurin, pero el punto es que el gradiente y la Hessiana todavía son desconocidos, y necesitamos encontrarlos. ¿Podemos hacerlo?
Sí, podemos. Tenemos mucha información y encontrar el coeficiente de v y H es un problema lineal. Para un 2 DOF, tenemos 1 incógnita "c", a incógnitas en el término lineal "v" y 2 + 1 en "H"porque H es simétrico. Para 3 DOF, tenemos 1 + 3 + 3 + 2 + 1 y así sucesivamente. Esto no es más que álgebra lineal. Nuestros miles de simulaciones y la pseudoinversión de More Penrose nos darán esas incógnitas más rápido de lo que podemos decir "solución numérica".
A lo bueno
Y es ahora que comienza lo interesante. Suponiendo que nuestras expansiones de segundo orden son buenas, hemos reducido miles de simulaciones a un modelo que ahora podemos desarmar aún más.
Lo primero que suele hacer uno tras obtener la expansión es comprobar en qué medida esta reproduce los miles de resultados simulados. Muy a menudo, la correlación entre el modelo y las simulaciones es superior a 99,1 %. Consideraría que un 95,1 % es apenas útil, pero el resultado habitual ronda el 99,1 % o más. Por supuesto, dependerá de cómo sea la propiedad subyacente, de si nuestro modelo numérico se refiere a una propiedad estadística o no.
Antes de jugar con este modelo, no lo sabíamos, pero aún no he encontrado un caso que no pudiera transformarse de alguna manera que permitiera que esta expansión capturara toda la varianza de nuestras simulaciones, esencialmente.
Análisis de la ampliación
Ahora llegamos a la parte en la que podemos cosechar los beneficios de nuestro duro trabajo. Típicamente hay tres tipos de resultados, o bien la expansión está dominada por el término lineal, o el término cuadrado o es mixta, que en realidad es bastante interesante porque nos dice que nuestra expansión no está alrededor de un mínimo.
Si domina el término lineal, pues ya está. No hay que hablar de interacciones entre los DOF. Caso cerrado. Nuestro sistema era sencillo, y si antes no lo entendíamos, ahora seguro que sí.
La cosa se pone más interesante cuando el término de segundo orden domina la expansión, porque ahora hay más cosas que aprender. Lo que hay que hacer aquí es definitivamente llamar más álgebra lineal en servicio y reescribir H como,
mediante la descomposición de valores singulares, abreviada SVD.
Si ha llegado hasta aquí y decide no aprovechar esta oportunidad, equivaldría a que Neo se tomara la píldora azul, optando por dormir y creer lo que él quiera creer. Nunca tomes la píldora azul.
Si tu sistema necesita expresarse en términos de una matriz de segundo orden, tienes que quedarte en el país de las maravillas y dejar que la SVD te muestre hasta dónde llega el agujero del conejo.
Esto no es solo un juego teórico de números. Es posible que necesites saber esto al diseñar tu óptica porque, no solo te dice que ciertas combinaciones de aberraciones deben optimizarse juntas, sino que los elementos diagonales de $\Sigma$ también te indican cuán importantes son realmente cada una de esas combinaciones, lo que es una pista invaluable sobre qué debe suprimir más la función de mérito.
Entonces, ¿qué ocurre con el caso mixto, en el que tanto la parte lineal como la parte cuadrada contribuyen significativamente al modelo? Éste es realmente interesante porque nos dice que, contrariamente a lo que creíamos al principio, el sistema no se expandió en torno al estado ideal.
Este caso requiere un poco de precaución porque la solución depende del modelo, e incluso así, puede apuntar a un nuevo mínimo fuera del volumen explorado por el conjunto inicial de puntos de muestreo. Todavía puede estar bien, pero no se puede dar por sentado.
Es la hora del ejemplo
Supongamos que aplicamos esta teoría a algo como el acoplamiento de fibra. Manteniendo el espíritu de que no sabemos cómo funciona, usamos los polinomios de Zernike como nuestros grados de libertad y, como nuestra función de prueba, calculamos la pérdida de inserción en función de nuestros grados de libertad.
Primero, definiríamos cuántos GRADOS DE LIBERTAD estamos interesados en estudiar. Digamos que nos detenemos en Z16. Sabemos que Z1 usualmente no importa, pero los que le siguen sí, por lo tanto 15 GRADOS DE LIBERTAD.
A continuación, generamos 1024 puntos de muestra sobre 15 grados de libertad usando LHS. El LHS generalmente genera puntos de muestra sobre un hipercubo, por lo que necesitamos escalar esos valores a algo razonable. Si no sabemos nada sobre el tema, entonces probablemente deberíamos empezar pequeño, muy pequeño. Luego, tal vez repetir el proceso hasta que encontremos que el modelo que calculamos ya no se ajusta muy bien a los datos, o hasta que alcancemos un rango de valores que creemos que son relevantes para nuestro sistema.
Ahora, saltamos un poco en el tiempo y 1024 simulaciones de pérdida de inserción después, tenemos nuestra función f(x,....) y algo que modelar. (Esta simulación asumió una apodización de 2 y un modo fundamental gaussiano. Este blog no trata tanto sobre fibras monomodo, así que perdone las suposiciones simplificadas sobre fibras monomodo.
Una vez que encontremos los coeficientes de c, v, y Hpodemos ver cómo el modelo ha captado nuestras simulaciones,
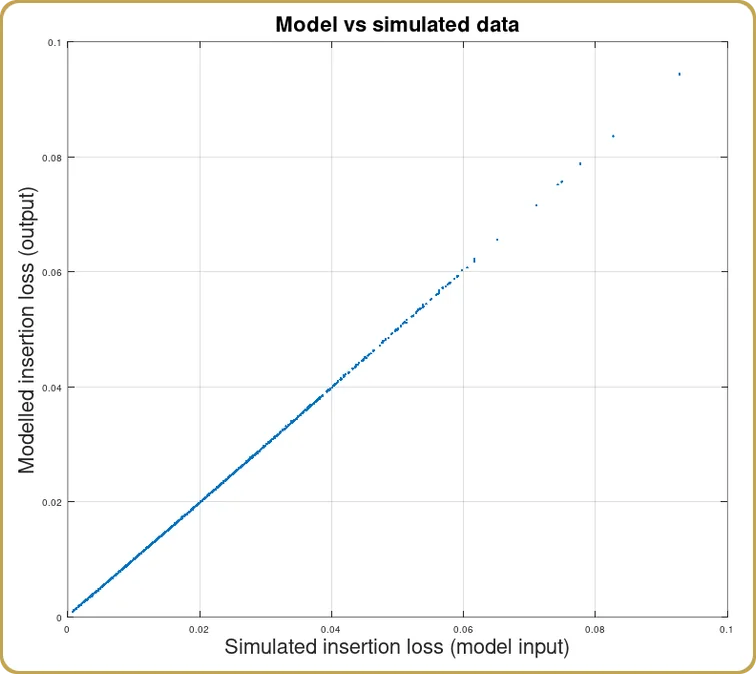
Como era de esperar, obtuvimos una buena correlación entre las simulaciones y la expansión del modelo. Dado que la óptica física solo se describe mediante la integral de solapamiento, era de esperar. Después de todo, se supone que este es un ejemplo del que aprender.
Ahora también podemos ver qué parte de esta correlación procede del término lineal,
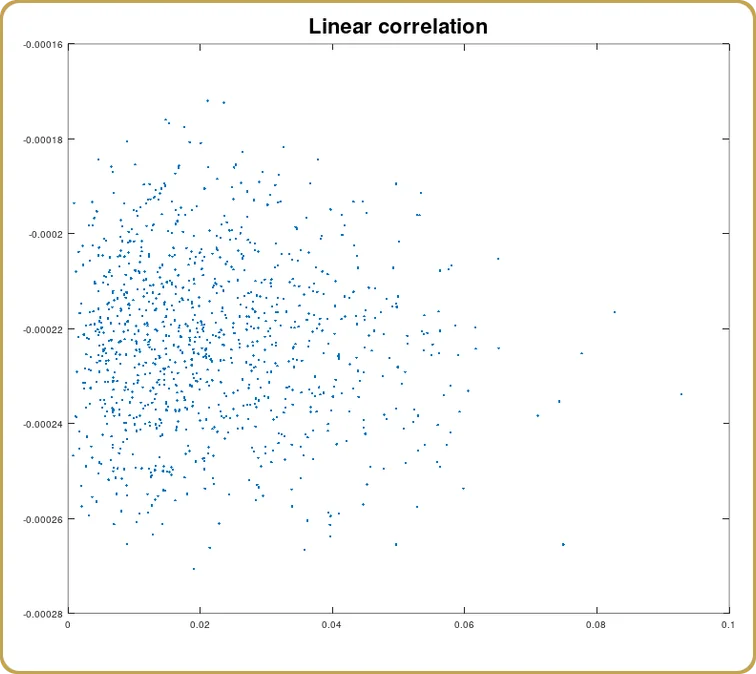
Y de nuevo, como se esperaba, la correlación es un cero (estadístico). Modelamos algo que tiene un mínimo en cero aberraciones. Se espera que la parte lineal desaparezca. Así que ahora, veamos el término cuadrado.
Espero que a estas alturas, sea bastante obvio que vamos a utilizar la Descomposición de Valor Singular, ¿recuerdas la píldora roja, verdad? Por lo tanto, lanzamos nuestro H en la SVD, y lo primero que hay que escudriñar son los valores singulares,
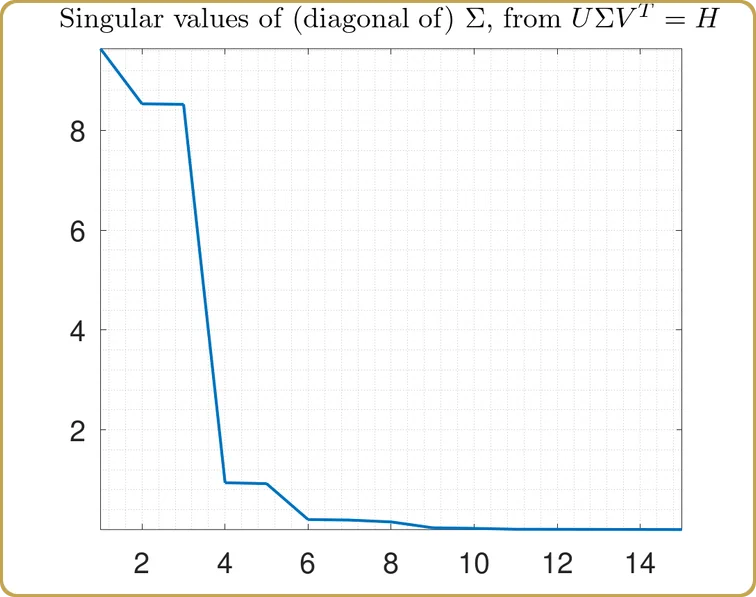
Los valores reales en el eje Y no son tan interesantes después de todo, dependen del volumen de nuestro hipercubo de prueba, que utilizamos para muestrear nuestro problema. Lo que es más interesante es la estructura. Nuestro problema se ha reducido a casi 3 variables independientes, más 2 mucho menos importantes. Echemos un vistazo,
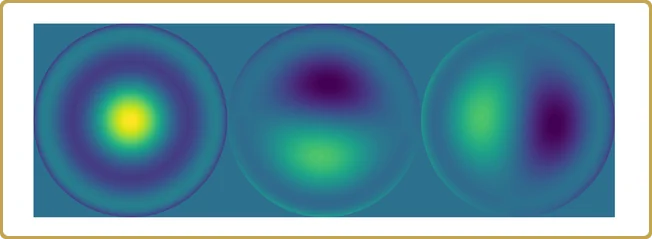
Es hora de resumir.
Empezamos con 1024 valores simulados en 15 dimensiones de algo que (fingimos) no sabíamos nada, y terminamos con 3 contribuciones principales a una propiedad que queríamos entender.
No es un resultado inusual cuando se realiza este tipo de análisis. Quizá la correlación no sea tan buena como en este ejemplo construido, pero con alguna transformación de los datos, el modelo de 2º orden puede capturar esencialmente toda la varianza de la simulación.
Quizás el aspecto más valioso de este tipo de análisis es que podemos asumir un número mucho mayor de grados de libertad y no limitarnos por nuestra capacidad para desentrañar la complejidad, o para conectarnos con la metáfora del mapa, no hay árboles. Solo vemos bosques y colinas. Desde este punto de vista, la imagen completa es todo lo que hay, y todo lo que pagamos por ella fue tiempo de computadora.
Herramientas para ingenieros de sistemas
Existe una herramienta práctica para ingenieros de sistemas que solo necesitan una forma de capturar una de las muchas partes móviles en su (generalmente bastante grande) hoja de Excel de compensaciones del sistema.
No es habitual encontrar un análisis tan clásico como el que aquí se presenta. Escribo esto porque acabo de toparme con un caso en el que no hay correlación lineal ni de segundo orden, pero la expansión completa sigue representando el 96,1 % de los datos. Esto no es inusual cuando se mezclan variables que no están relacionadas físicamente entre sí. Por lo general, no se modelan bien juntas.
Sin embargo, la expansión aún capturó información que puede ser utilizada cuando nosotros, como ingenieros de sistemas, necesitamos intercambiar entre parámetros que capturamos en nuestras simulaciones (digamos) ópticas frente a los efectos que estos parámetros pueden tener en otras propiedades del sistema. Muchos ejemplos de este tipo.
Ir más lejos
¿Por qué nos detuvimos en una expansión de 2º orden? Bueno, hay “razones”. El siguiente orden viene descrito por un tensor simétrico de rango 3. Todavía podemos extraer los componentes de este tensor porque el problema de mínimos cuadrados que acopla estos componentes a nuestros datos sigue siendo lineal.
Sin embargo, perdemos algunas cosas. No hay SVD para tensores, por ejemplo. Sin embargo, hay trabajos matemáticos “recientes” realizados aquí (si se llama reciente a 2005, pero yo empecé a hacer esto antes de 2005, así que), que pueden ofrecer más ideas sobre las propiedades de los sistemas complejos, como los valores y vectores propios para tensores.
Si te parece demasiado esotérico, y lo entiendo perfectamente si es así, una expansión de tercer orden garantiza capturar más varianza en tus datos que una de segundo orden. Si solo necesitas esa función mágica en tu hoja de Excel, al menos puedes tenerla.