Coherencia

La coherencia es quizá la propiedad más interesante de la luz y podría decirse que los efectos de la interferencia son el núcleo de lo que consideramos el campo de la óptica. Sin embargo, no hay que buscar demasiado para encontrar un especialista en óptica que simplemente no quiera saber nada de ella. En la práctica, a menudo necesitamos la cantidad adecuada de coherencia, pero como se trata de un objeto un poco rígido, no podemos estirarlo, pero a menudo podemos trocearlo y desplazarlo. Esto hará que la densidad espectral sea discreta y la función de coherencia periódica. A continuación se dan dos ejemplos de ello.

Láseres de diodo modulados por RF

Los láseres de diodo modulados por RF son una herramienta muy útil que hay que tener en el metrología caja de herramientas. Cuando montamos el interferómetro clásico de Twyman-Green (al que muchos se refieren como el interferómetro de Michelson y Michelson se refirió a él como esencialmente inútil, pero entonces conseguimos el láser), un poco de alineación cuidadosa y hemos conseguido crear un par de etalones. Obviamente, esto no es genial. No son grandes etalones, pero no deberían existir en absoluto.

Podemos evitar casi por completo todos esos etalones si tuviéramos una fuente con una longitud de coherencia corta y esto es lo que el diodo modulado por RF, llamémoslo así, intenta emular. La modulación RF (profunda) impedirá que domine un único modo y, en su lugar, todos los modos de la cavidad con una ganancia superior a la unidad emitirán luz, y en lugar de 1 a 3 modos tendremos ahora un espectro discreto de frecuencias espaciadas uniformemente y, en consecuencia, una función de coherencia periódica.

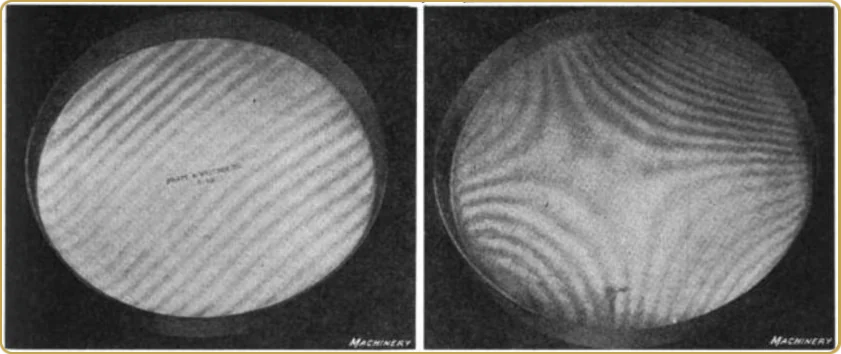
Si ahora montamos un interferómetro Twyman-Green con un espejo sobre una platina (preferiblemente de gran recorrido) encontraremos, muy probablemente, cero franjas hasta que con algo de paciencia movamos uno de los espejos hasta que veamos franjas de contraste 100%. Y entonces movemos el espejo 100-150 micras y las franjas desaparecen por completo, pero si continuamos otros 10, tal vez 15 milímetros, volveremos a encontrar franjas de contraste 100%, y de nuevo tras otros 10 a 15 milímetros. Se trata de una consecuencia bastante sorprendente del teorema de Wiener-Khinchin, que relaciona la densidad espectral de una señal en el espacio de frecuencias y su autocorrelación (en el tiempo), que son pares de Fourier.

Coherencia espacial

Al igual que la coherencia longitudinal de una fuente puntual viene determinada por la dispersión en frecuencias de la fuente de luz, la coherencia espacial (o transversal) viene determinada por la dispersión en ángulos de incidencia. La coherencia espacial sigue, por así decirlo, las leyes ópticas habituales. Si la reimaginamos con algún aumento, el producto de la extensión espacial (transversal) y la dispersión en los ángulos de incidencia se conserva, hasta la fuente. Podemos disminuirlo con aperturas, pero no podemos aumentarlo, al menos no con superficies en las que se aplica la ley de Snell.
De vuelta a la fuente láser, solemos darnos cuenta de que este producto no es lo suficientemente grande y el truco habitual con, por ejemplo, los láseres Excimer es utilizar la longitud de coherencia longitudinal corta para obtener una longitud de coherencia espacial más corta en una de las direcciones en las que suele ser demasiado corta. Incluso después de este truco, el producto es demasiado pequeño, pero como de todos modos necesitamos un homogeneizador, añadimos un conjunto de lentes (2D) que extiende los ángulos de incidencia disponibles a cualquier rango deseado.

Como en el caso del diodo modulado por RF, volvemos a tener un conjunto discreto de fuentes, esta vez en el espacio, pero se aplica la misma relación entre autocorrelación y densidad espectral y volvemos a tener una función de coherencia periódica (esta vez espacial). Normalmente, cuando construimos un homogeneizador, si obtenemos una iluminación plana podríamos pensar que hemos terminado. Si el dispositivo que estamos construyendo está pensado para el entretenimiento, como un proyector DMD/DLP, probablemente sea cierto, pero si estamos construyendo un dispositivo de alta precisión en el que los detalles importan, probablemente también tengamos que asegurarnos de que la densidad espectral que se transforma en el homogeneizador es uniforme, o por poner una analogía, si estamos iluminando un modulador y nos imaginamos caminando sobre su superficie mirando hacia arriba, hacia el conjunto de lentes, queremos ver cada fuente (como mínimo) exactamente a la misma intensidad, sin que parpadeen como las estrellas cuando nos movemos. Si lo hacen, nuestra función de coherencia varía sobre la superficie iluminada y, aunque nuestra iluminación sea uniforme, las propiedades de imagen no lo son.

La periodicidad de la función de coherencia resultante no carece de consecuencias y debemos tener suficientes fuentes (microlentes) en ambas direcciones para que el periodo sea lo suficientemente largo como para que sea suprimido por la resolución óptica de la lente de proyección que probablemente (tendremos) más abajo en el eje óptico.

Hay dos referencias que cubren la mayor parte de lo que uno necesita saber y ambas son de Goodman, pero no el mismo Goodman. Una es Óptica estadística por Joseph Goodman. Casi todo el mundo lo conoce. El otro es del poco menos conocido Douglas Goodman, "Métodos gráficos para ayudar a comprender las imágenes parcialmente coherentes". No puedo recomendarlos lo suficiente.