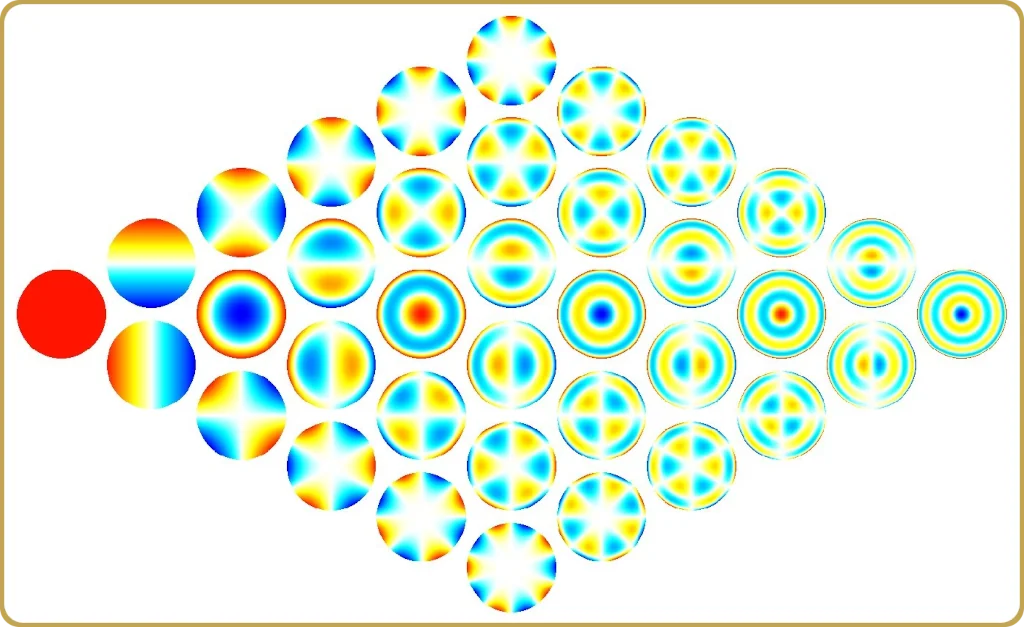
Los polinomios de Zernike, todos los reconocemos y son el lenguaje del que hablamos a menudo cuando describimos sistemas ópticos. Pero, ¿son siempre el lenguaje correcto?
¿Hay un lenguaje equivocado? Al final, intentaríamos llevar un diseño a cero para que no importe. Pero bueno, cero, eso sería como no decir nada.
¿Qué pasa si no podemos llegar a cero, o si en el tolerado podemos elegir empujar este o aquel término, pero no ambos? ¿Cómo elegir? Si estamos fabricando un telescopio, el caso está claro. Queremos minimizar la varianza de la fuente de ondas y, por tanto, maximizar la relación Strehl. Muy claramente derivado en Born & Wolf.
Sin embargo, ¿qué ocurre si la propiedad que nos interesa no se deriva de la varianza? ¿Cómo podemos saberlo?
Un análisis que se puede emplear es encontrar la expansión MacLaurin de la propiedad de interés a segundo orden usando el polinomio Zernike como (digamos) sondas o simplemente parámetros libres. Para ello, se puede utilizar un enfoque de Monte Carlo o un enfoque de muestreo de hipercubos latinos, y cuál es el mejor es un debate para tener en otra parte. Sin embargo, una vez que hemos hecho eso, podemos encontrar el c, v, y A que hacen el mejor ajuste a los datos, y este ajuste puede ser realmente muy bueno.
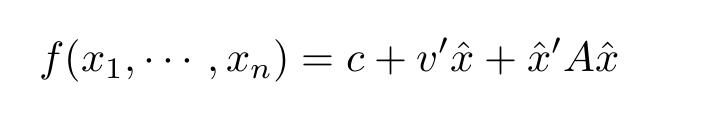
Si A resulta no ser diagonal en esta expansión, entonces los polinomios de Zernike no son el lenguaje adecuado porque no se deduce que minimizar uno de los coeficientes mejore siempre nuestra propiedad de interés. En este caso, diagonalizar A nos dará una nueva base ortogonal.
Sin embargo, antes de plantearnos la pregunta de cuáles de los términos minimizar, pero en la nueva base, qué pasa con el término lineal v. La respuesta es: depende. Evidentemente, existe la posibilidad de buscar la solución a f = 0 y si esta solución se encuentra dentro del intervalo de validez de la expansión, probablemente hemos encontrado una solución no trivial en la que las aberraciones distintas de cero generan un error nulo. Esto ocurre, pero muy a menudo v es esencialmente cero o la solución de f = 0 no está dentro del alcance de la expansión.
Cuando el término lineal v es cero, ahora nos haríamos la misma pregunta que al principio, debemos mejorar este o aquel término en la nueva base, la respuesta es, no importa porque mientras reduzcamos la suma incoherente (en cuadratura) de ellos, nuestra propiedad de interés mejora.
Podría decirse que se trata de algo esotérico, pero si disponemos de los modelos de nuestro sistema óptico y de la propiedad que nos interesa, puede ser totalmente factible sondear entre 15 y 20 parámetros libres mediante unos cuantos miles de simulaciones y obtener información valiosa sobre los fundamentos del sistema óptico. A menudo, esto puede hacerse en menos de un día si ya disponemos de los modelos.




Deja un comentario