Interferómetro de difracción puntual

El interferómetro Smartt o su evolución, el interferómetro de difracción puntual con desplazamiento de fase, es probablemente el más preciso que se puede fabricar, y ni siquiera es caro. Tiene su limitación, no todo, como que necesitamos un foco para crear una onda de referencia con un agujero de alfiler. Si el foco está a una apertura numérica alta, el estenopo puede ser realmente pequeño, por lo que hay que tener en cuenta la posibilidad de que se evapore cuando realmente queramos utilizarlo. Pero todo eso puede superarse con un poco de ingeniería cuidadosa, sobre todo con fuentes pulsadas como los láseres Excimer o Q-switched. En el caso de los agujeros de alfiler de tamaño micrométrico, probablemente no haya ningún problema, porque aún tenemos que ajustar la exposición para registrar el interferograma en una cámara, que suelen ser muy sensibles.

Otro inconveniente es que no se trata de un interferómetro flexible. Se trata más bien de una herramienta hecha a medida para sistemas específicos. Dicho esto, no es caro de hacer, un agujero de alfiler, un actuador y otro (off-the-shelf) agujero de alfiler que incluso puede ser modificado en su tienda local de mecánica de precisión. Esto es lo que hice la primera vez que necesité uno. Con menos de 5k a 8k de actuador y pinholes, y algo de software tenemos una herramienta que es al menos lambda/200 o incluso lambda/300 precisa y lambda/500 a lambda/2000 estable, dependiendo del tamaño de la apertura y el ambiente térmico donde se encuentra el interferómetro.

Precisión

Que yo sepa, este nivel de precisión no puede obtenerse de ninguna fuente comercial. Probablemente, también deberíamos matizar la afirmación de la precisión lambda/300. Dado que el interferómetro de difracción puntual crea su referencia utilizando cualquier frente de onda que se esté midiendo, la referencia sólo será una onda perfectamente esférica si el agujero de alfiler se ilumina con una onda perfectamente esférica. En realidad, se trata más bien de un interferómetro con una precisión de 3-3,5% para ópticas en el límite de difracción o por debajo. Algunas aberraciones se suprimen más (como la esférica o la potencia) y otras menos (como el coma). Por tanto, el número 3-3,5% es algo así como la media de un conjunto, y como el valor RMS para el frente de onda en el criterio de Rayleigh es del orden de 0,07 a 0,08 (dependiendo del frente de onda), llegaremos a algo así como 1/0,075/0,035 = 380. En la práctica, hay alguna variación del operador al alinear y enfocar el estenopo, y algunas otras cosas.

En la práctica, se pueden ver los efectos de la deformación de los elementos de la lente cuando se montan con una fuerza mecánica ligeramente diferente. Este interferómetro parece casi una herramienta matemática. No me malinterpreten, me gustan los sensores Shack-Hartmann. Cuando se utilizan para el trabajo adecuado, no hay nada mejor, pero cuando intentamos llevarlos por debajo de 10 nm RMS, se requiere mucho control sobre los errores sistemáticos. Con el interferómetro de difracción puntual, prácticamente no hay dudas. Lo que se ve es lo que hay.

El desplazamiento de fase se realiza con una rejilla gruesa (tipo Ronchi) y la principal elección de diseño es si el frente de onda se va a medir a través del 0º o del 1º orden de difracción. Podemos elegir medir con o sin lente de proyección de franja, pero si optamos por no tener una, se hace difícil identificar la pupila que define el sistema óptico que se está midiendo. Por lo tanto, es preferible disponer de una óptica de proyección de franjas, pero eso, por supuesto, nos obliga a responder a la pregunta sobre el error de medición añadido por la óptica situada entre el estenopo y la cámara.

Si elegimos medir a través del orden 0 con un recuento de franjas elevado (que establece la resolución de este instrumento), tendremos que calibrar la proyección de franjas utilizando dos agujeros de alfiler, lo que resulta algo difícil porque ahora debemos hacer pasar dos focos a través de dos agujeros de alfiler al mismo tiempo. Este par de agujeros de alfiler deberá fabricarse a medida si necesitamos la máxima precisión posible del frente de onda. Por otro lado, obtendremos resultados bastante precisos sin calibrar, especialmente si la óptica de proyección de franjas está corregida para el coma, bien alineada y el recuento de franjas (resolución del interferómetro) no es demasiado alto, digamos 50-70 franjas.

Compromisos

Si el objetivo es la mayor resolución posible y una óptica simple de proyección de franjas, podemos medir a través del 1er orden. La ventaja de esto es que podemos obtener un contraste de franjas cercano al 100%, lo que parece bonito pero realmente no es tan crítico, pero lo que es más importante, la calibración se realiza utilizando una rendija que aísla el 0º y el 1º orden de difracción que se utilizan durante la medición. Esta abertura es muy sencilla de fabricar o comprar como componente estándar. Pero en este caso, tenemos que calibrar. El interferómetro mostrado aquí es de este tipo. La lente de proyección de franjas no es más que un singlete plano-convexo con una distancia focal que adapta el tamaño de la imagen de la pupila a la cámara. La sencilla calibración se encarga del coma lineal (y de los efectos de difracción cónica si la rejilla está en el haz convergente) y mientras no movamos el estenopo, no tendremos que recalibrar, por eso está todo en su propia mesa que se puede mover sobre el campo. Cuando es necesario, la calibración es un procedimiento de un minuto.

Este es, sin duda, mi montaje de interferómetro favorito. Hay cosas que hay que hacer correctamente, como asegurarse de que las ranuras de la rejilla de transmisión están rectas. En este caso particular, la rejilla fue fabricada a Chalmers MC2 en una oblea de monosilicio grabada mediante el proceso Bosh (pero hay otras formas), y como pequeño truco, se puede verificar la rectitud de las ranuras utilizando el interferómetro sin tocar la rejilla.

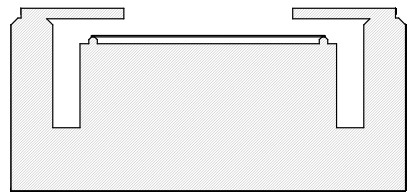
Acerca de la imagen

Esta configuración en particular medía un relé desmagnificador de 60 kg con una distancia de trabajo de 600 mm a una NA de aproximadamente 0,05. No había ninguna forma práctica de acceder a su plano de Fourier. No había forma práctica de acceder a su plano de Fourier, por lo que el interferómetro se encuentra totalmente fuera de este sistema óptico.

Para terminar con una anécdota, ese relé de 60 kg acabó en esa mesa óptica porque su fabricante no pudo verificar su funcionamiento. Había razones para creer que estaba desalineado, pero nadie sabía qué y cuánto. Tras un barrido de 15 minutos sobre el campo, apareció una línea perfectamente recta sobre el campo en Z6 a unas 150 mili ondas en los puntos extremos. Clásico. Unas pequeñas pruebas en Zemax revelaron que mover la imagen 0,8 mm inclinando un espejo debería invertir la Z6 lineal, así que eso fue lo que hicimos. Bingo. No más Z6 lineal. Como si se anulara matemáticamente. Por eso me encanta este interferómetro. Es una herramienta tan limpia con la que trabajar.