Cómo hacerlo: Moduladores espaciales de luz

Acerca de esta charla técnica

Los moduladores espaciales de luz (SLM) son componentes ópticos activos que pueden alterar la amplitud, fase o polarización de un haz de luz. En esta charla técnica me centraré en un subconjunto concreto: los que lo consiguen mediante una matriz bidimensional pixelada. Aunque esto no abarca todos los tipos de SLM, es una categoría lo suficientemente amplia e interesante como para explorarla. Dado que este blog se centra en los integradores de sistemas, también destacaré las consideraciones clave si decide incorporar un SLM a su sistema.

Reflexivo o transmisivo

Para empezar, tenemos dos grandes subclases, las reflectantes y las transmisivas. La mayoría de las SLM de interés industrial son del tipo reflectante. La razón es sencilla. Los dispositivos de alto rendimiento requieren una oblea CMOS para distribuir los datos por el dispositivo. La forma más sencilla de conseguirlo es colocar una capa metálica directamente sobre la oblea. Es posible disponer una superficie ópticamente transmisiva que pueda distribuir una señal eléctrica, pero eso implica electrones libres y éstos tienden a interactuar con la luz transmitida. La compensación que esto implica suele afectar a la velocidad del dispositivo o a la transmisión óptica.

Dicho esto, todavía se pueden encontrar muchos productos técnicamente interesantes que utilizan este principio tanto en aplicaciones de consumo (como las pantallas LCD y algunos proyectos basados en LCoS) como en entornos industriales.

SLM de amplitud reflectante

Se trata de una clase importante de moduladores espaciales de la luz. Cabe destacar que La DLP de Texas Instruments de esta clase. Aunque este tipo de SLM alteran la fase de la luz reflejada, no se utilizan como tales. Me explico. El DLP es un dispositivo de microespejo puramente reflectante en el que cada microespejo sólo puede tener dos estados estables que alteran entre más o menos 12 grados a lo largo de su diagonal, aunque el ángulo puede variar entre varios tipos. Cada punto de la superficie de este dispositivo altera la fase de la luz introduciendo una diferencia de camino óptico, pero como estas fases no son independientes, sólo podemos observar el efecto neto de un pequeño espejo inclinado.

Existen otros SLM que funcionan según el mismo principio óptico, como el Espejo inclinable analógico IPMS SLM. Dado que los dispositivos de espejo inclinable son en general de fase neutra, dependen del sistema de formación de imágenes para expresar el efecto deseado. Sin él, sólo parecen una superficie reflectante rugosa. Con un sistema de proyección correctamente diseñado, se convierten en sistemas de generación de patrones de alto rendimiento que no pueden distinguirse de las máscaras binarias de alta calidad.

Los dispositivos analógicos de espejo inclinado son fáciles de calibrar y sencillos de utilizar, pero requieren un láser Excimer para alcanzar su verdadero potencial. Sin embargo, hay algunas propiedades que aporta un espejo inclinado en el plano de la imagen que merece la pena tener en cuenta. La inclinación de un espejo aislado nunca puede ser ocultada por el sistema óptico, incluso si la óptica de proyección no está ni siquiera cerca de resolver el micro-espejo. Esto puede utilizarse a veces para ajustar correctamente el enfoque, posiblemente incluso la forma más sensible de hacerlo sin un interferómetro o un sensor de frente de onda, pero probablemente sólo sea útil a resoluciones más bajas.

La teoría de Fourier al rescate

Para utilizar un dispositivo de espejo inclinable de este tipo en aplicaciones de gama alta, la inclinación del espejo debe ser alterna (como en la figura anterior). La óptica de proyección anulará entonces la fase. En general, estos dispositivos se entienden mejor utilizando la teoría de Fourier.

He aquí un ejemplo: Un dispositivo con espejos planos tiene un contraste infinito, sólo hay que inclinar los espejos hasta el ángulo correcto. La placa (o espejo) inclinada tiene un patrón de reflexión dado por la función sinc y el cero de esa sinc es el ángulo correcto para un contraste infinito. ¿Qué ocurre cuando utilizamos una iluminación parcialmente coherente, y la SLM se ilumina con un rango de ángulos incidentes? ¿Significa eso que el contraste se degrada con la iluminación parcialmente coherente? Si nos ceñimos a la imagen sinc, podemos pensar que es imposible conseguir un ángulo de inclinación óptimo, ya que no podemos adaptar simultáneamente un ángulo de inclinación a una gama de ángulos de incidencia. En cambio, si optamos por el enfoque de Fourier, el conjunto iluminado con incidencia cero refleja toda la luz a lo largo de la normal. El efecto de la inclinación se representa como un conjunto de modos de difracción que no se van a transmitir a través de la pupila. Para cualquier onda plana fuera del eje, la luz reflejada no es más que una réplica desplazada del patrón en el eje. Si el primero tenía un contraste infinito (visto a través de la óptica de proyección), también lo tiene la réplica. El enfoque de Fourier da la respuesta correcta.

Defectos comunes de los dispositivos

Los dispositivos MEMS nunca son perfectamente planos. Cuando se resuelve la superficie pulida sobre la que están fabricados, se produce una liberación mecánica de fuerzas que añade un desplazamiento vertical de corto alcance. Esto introduce un moteado parcialmente desarrollado y otros efectos. Establece el límite de la calidad de imagen cuando se utilizan estos dispositivos. No todos los fabricantes dan especificaciones sobre estos efectos. Por ejemplo, no he podido encontrarla para el Ti DLP. Sin embargo, algunos límites de este parámetro vienen dados por la eficacia de la difracción. Dado que el DLP debe superponer muchas imágenes para generar una escala de grises, el moteado parcialmente revelado no debería contribuir significativamente a la degradación de la calidad de la imagen cuando se utilizan estos dispositivos.

Con el tiempo, sobre todo cuando se utilizan longitudes de onda cortas, la superficie superior puede sufrir cierto recocido y compactación que provoque cierta curvatura de los espejos. En el caso de los DLP, esto tiene un efecto insignificante en la calidad de la imagen debido a la gran inclinación. Para los dispositivos analógicos, ésta es probablemente la propiedad que fija la vida útil del dispositivo. Es visible como degradación del contraste, pero afecta a otras propiedades importantes de la imagen, como la sensibilidad de enfoque.

SLM de amplitud lineal

Los moduladores lineales o unidimensionales probablemente merezcan su propia página, pero intentaré resumir aquí lo esencial hablando de dos dispositivos muy diferentes. Uno es el Silicon Light Machines Grating Light Valve, o GLV para abreviar. El otro es el Fraunhofer IPMS 8k mostrado en este documento.

Lo que hace interesantes a los moduladores 1D es que pueden utilizar una fuente láser continua o casi continua. En el caso del GLV, puede incluso utilizar un láser de conmutación Q. Esto resulta muy atractivo desde el punto de vista del coste del sistema. Aunque la frecuencia de repetición del GLV es alta para un láser de conmutación de Q, sigue habiendo buenas opciones. El principal inconveniente del GLV es la forma en que genera la escala de grises.

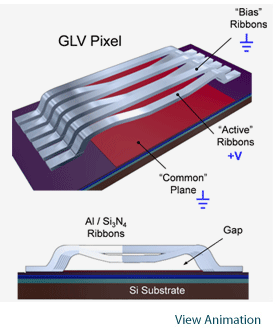
La escala de grises se genera creando una rejilla con una profundidad variable y, por tanto, una magnitud variable de luz difractada. Este dispositivo puede utilizarse tanto en orden 0 como en orden 1, pero tiene un contrato significativamente mejor en orden 1. Algunas variantes del dispositivo combinan dos cintas para formar un píxel, mientras que otras utilizan 6 o 3 pares de cintas. Esto no tiene ningún efecto significativo en las propiedades ópticas de la imagen.

Lo que es esencial tener en cuenta, sin embargo, es que este enfoque acopla la amplitud reflejada y la fase, lo que para la litografía es crítico porque causa una sensibilidad de enfoque si el dispositivo se utiliza para la escala de grises (que es la mayoría de los casos). Otra consecuencia, quizá no tan crítica, es que el mínimo de reflexión no se puede calibrar si el dispositivo se utiliza en orden 0. Cabe preguntarse cómo se calibra un SLM que no refleja nada de luz, o muy poca. Digamos que el SLM de espejo inclinable puede calibrarse fácilmente, mientras que el GLV sobrevive a esto simplemente por no ser muy sensible cuando se opera cerca de la amplitud reflejada cero. Como seque al dispositivo Fraunhofer mencionaremos que la GLV necesita ser iluminada por una línea estrecha, de 5-10 micras de espesor. Esto significa que debemos tener en cuenta la densidad de potencia pico cuando utilicemos este dispositivo.

¿Cómo resuelve esto el dispositivo Fraunhofer? Este dispositivo se desarrolló desde el principio para manejar fuentes continuas de alta potencia. Por lo tanto, el dispositivo es ópticamente plano en toda su superficie de 80×2 mm.² superficie. Para aprovecharla, la SLM debe colocarse antes o después del mejor enfoque. Para evitar una óptica demasiado cilíndrica, se puede restablecer una imagen libre de astigmatismo insertando una o dos placas paralelas inclinadas.

Como este dispositivo utiliza espejos basculantes, es de fase neutra y no muestra ningún efecto de enfoque pasante cuando se utiliza como SLM de escala de grises. Antes de pasar a la siguiente sección, hay que mencionar que, al menos en algún lugar de Internet, este modulador se diseñó para una frecuencia de cuadro de 2 MHz, no de 1 MHz como el documento vinculado (y la publicación al respecto). La razón por la que podemos conducir un dispositivo por encima de su frecuencia de resonancia nominal es que el modulador se diseñó para un factor Q bastante bajo, de aproximadamente 1, y un dispositivo de escala de grises no puede resolver píxeles individuales de todos modos. Normalmente, un buen diseño suele resolver de 3 a 4 píxeles, dependiendo de cuánto valoremos la calidad de la imagen. Estas dos opciones de diseño permitieron a Micronic controlar este modulador a 2 MHz. Con un píxel de 1,25um (en esa dirección) se conseguía una velocidad de escritura de 2,5 m/s. Era algo digno de ver.

SLM de fase reflectante

Las SLM de fase reflectante crean una diferencia de longitud de trayectoria principalmente de dos maneras. Desplazando la superficie reflectante o cambiando localmente el índice de refracción para generar una diferencia de longitud de trayectoria. El primer caso describiría moduladores espaciales de luz como el RealHolo, el PLM de Texas Instruments o el PLV de Silicon Light Machines. En términos de potencial técnico, el RealHolo destaca claramente entre los MEMS.

Cristal líquido sobre silicio - LCoS

Otra tecnología de fase SLM muy popular es la de cristal líquido sobre silicio (LCoS). Estas micropantallas se basan en una pila bastante compleja de tecnologías, que incluye una placa base CMOS, una capa metálica de píxeles, capas de alineación superior e inferior para el cristal líquido, una capa de óxido de indio y estaño (ITO) para generar el campo eléctrico a través del cristal líquido y una cubierta de vidrio para sostener el ITO. A pesar de esta complejidad, los fabricantes pueden producir paneles LCoS en grandes volúmenes con altos rendimientos y mínimos defectos en los píxeles.

Los paneles LCoS ofrecen varias ventajas, entre ellas la robustez. Sin embargo, también presentan inconvenientes, como la dependencia de la polarización. Además, el grosor de la capa de cristal líquido, determinado por la longitud de onda para la que está diseñado el SLM, limita la resolución efectiva del modulador. Esta limitación se debe a la naturaleza de los campos eléctricos, que tienden a divergir a medida que se propagan desde su fuente. Los paneles LCoS son, en esencia, condensadores transparentes densamente empaquetados, y cuando el tamaño lateral de cada condensador es menor que la distancia entre sus placas, el campo eléctrico se extiende a los píxeles vecinos, creando interferencias cruzadas. En la industria LCoS, este fenómeno se conoce como efecto de campo de franja. Provoca tanto efectos de polarización no deseados como disclinations. Antes de hablar de las SLM MEMS, debemos mencionar una gran ventaja: hoy en día se pueden adquirir en empresas como Hamamatsu o Fotónica Holoeye.

Conjuntos de espejos de pistón MEMS

Aunque los dispositivos pistón-MEMS no son tan raros como los unicornios, no es fácil ver uno en la naturaleza. Dicho esto, existen y si Texas Instruments acaba lanzando el PLM, es posible que lleguen a ser bastante comunes. Los dispositivos de pistón son realmente flexibles desde el punto de vista óptico. No hay efectos de polarización de los que hablar. No dependen de la longitud de onda siempre que iluminemos con una longitud de onda cada vez. Son rápidos y la fase es estable. Con los LCoS, hay que cambiar con frecuencia la polaridad de la tensión de alimentación para evitar la degradación del cristal líquido. Aquí nada de eso. Modulación de fase de 360 grados y sin interferencias de las que hablar. Estupendo. ¿Puedo tener un montón? Hay un problema, que es igualmente válido para los paneles LCoS, ¿cómo decidir qué fase fijar en cada píxel iluminado?

Generación de imágenes con dispositivos de sólo fase

Normalmente, recurrimos al algoritmo de Gerchberg-Saxton cuando necesitamos resolver este problema. Es especialmente útil en aplicaciones visuales, donde el cerebro hace que el resultado sea más apetecible. Una gran ventaja de los dispositivos de modulación de fase es que no necesitamos óptica. Ilumina con un haz suficientemente ancho y tendrás un proyector de dos partes, fuente de luz y SLM. La longitud de onda y el tamaño del píxel limitan su extensión angular, pero si es suficiente, ya está. Si no, podemos utilizar un telescopio galileano para obtener el aumento deseado.

Para la litografía, donde la calidad de la imagen lo es todo, tenemos que controlar la fase reflejada de la luz. Si no lo conseguimos a larga distancia, los objetos se desplazan. Si no lo conseguimos a corta distancia, los objetos se motean y, además, aumentan con las aberraciones de la óptica de proyección.

Sin embargo, hay que tener en cuenta otra cosa. ¿Cómo decidiremos la fase que hay que fijar para cada píxel? Los métodos de recuperación de fase son iterativos y, que yo sepa, devuelven una fase proyectada aleatoria. Los métodos directos que conozco utilizan redes neuronales, pero no he visto qué calidad de imagen podemos esperar de ellos. Yo esperaría que el enfoque de la red neuronal reprodujera, en el mejor de los casos, los resultados de los métodos de recuperación de fase utilizados para entrenarla. En consecuencia, esperaría que esos métodos generaran una fase aleatoria.

Algunos fundamentos teóricos

En el tema de la generación de patrones de alta calidad con moduladores de sólo fase, debemos identificar al menos dos casos, uno que es el caso de mapeo lineal, y el otro, un mapeo no lineal. El caso del mapeo lineal corresponde al mapeo lineal entre el modulador y la amplitud de la imagen de las imágenes coherentes, mientras que el caso no lineal se aplica a las imágenes parcialmente coherentes.

Para la imagen coherente, sabemos que la amplitud de la imagen es una "función" lineal de la amplitud reflejada,

Y cuando P representa un dispositivo discreto, podemos convertir la integral en una suma integrando sobre los "píxeles",

Hay detalles al respecto que creo que podemos omitir por el momento. Sin embargo, sabemos que, de un modo u otro, podemos invertir esta relación,

En la práctica, la inversa de H suele ser un pseudoinverso y así sucesivamente. No se trata de eso. Sin embargo, incluso para el caso simple en el que la respuesta al impulso H es real (es decir, parte imaginaria cero) y la amplitud que queremos resolver también es real, la solución (p) es entonces real. No es exactamente una gran solución para un dispositivo de pistón.

Los pistones necesitan un mapa del círculo unitario complejo

Entonces, necesitamos una forma de transformar un vector real p (con NxM elementos, donde NxM es el tamaño de nuestro SLM) en un vector,

donde el vector h tiene el mismo tamaño que p. Queremos las alturas, h, para tener la propiedad de que,

es decir, queremos cancelar la parte imaginaria utilizando el sistema óptico. Ahora bien, no es mi intención convertir este blog en un artículo de matemáticas, pero un sistema de imagen bien diseñado destinado a la escala de grises dejará bastante margen para soluciones h que coincidan con las imágenes generadas por la cartografía Hp.

Si la cartografía es lineal, como ya se ha dicho, la cancelación de la parte imaginaria puede hacerse perfectamente. Si no lo es, todavía hay una solución sencilla que nos acerca bastante a una solución decente. El camino es más o menos así. Supongamos que tenemos un conjunto de valores de gris (reales). Digamos que los obtuvimos pixelando una imagen vectorial. Donde las figuras de esa imagen cubrían un píxel por completo, asignábamos un valor de 1 al píxel, donde no lo cubría en absoluto, asignábamos 0, y donde lo cubría parcialmente, le dábamos un valor x que era de alguna manera representativo de cuánto cubría el píxel el objeto vectorial. Ahora, ¿cómo convertimos ese valor real x en una fase compleja? Bueno, podemos promoverlo a una amplitud compleja de longitud unitaria por,

Está al menos en el círculo de la unidad. Sin embargo, si lo intentamos, no nos dará lo que queremos. Pero, y ya sabes lo que dicen de los "pero", ¿por qué el signo más? Un signo menos es igualmente válido.

Aunque tampoco es la solución que buscamos, muestra que, para cada píxel, tenemos la libertad de elegir el signo de la parte imaginaria. Entonces, ¿qué tal elegirlo de forma que se filtre por la apertura?

Los índices, k y l, sólo están ahí para recordarnos que la SLM es una estructura 2D, y que tenemos la libertad de asignar cualquier signo que queramos a cualquier píxel de nuestra SLM y si elegimos los signos de forma que la parte imaginaria se anule en el sistema de proyección, este dispositivo de sólo fase producirá una imagen bastante bonita sin más esfuerzo que éste.

Para un sistema de imágenes coherente, podemos hacerlo un poco mejor con un esfuerzo bastante grande y para uno parcialmente coherente, este es un estado inicial para un esfuerzo igual, si no mayor, pero es un comienzo.

Cuando el cielo no es el límite SLM

El modulador de pistón aplicado a la litografía es el modulador definitivo para quienes desean llevar la resolución de sub-longitud de onda más allá de sus límites prácticos, pero tiene un coste. He aquí la cuestión. Un modulador de pistón puede proyectar cualquier fase y amplitud (en términos relativos), pero para la litografía, en realidad no queremos ninguna amplitud. Queremos que la imagen tenga una fase constante en toda la imagen porque una variación de fase es una variación de las dimensiones de la característica o la colocación a través del enfoque, y absolutamente no queremos eso. Esto significa que tenemos que invertir tiempo para encontrar una solución que restrinja ese grado de libertad particular de este modulador.

Tener el pastel y comérselo, Micronic inventó un espejo basculante diseño que incluía un paso de un cuarto de longitud de onda en la mitad del espejo. El resultado era una amplitud de imagen que podía alcanzar un rango (relativo) de -1 a 1 y una variación de fase nula. Todo lo bueno para lo que se necesitaba el espejo de pistón sin tanto trabajo. El inconveniente era una reducción de la reflectividad del dispositivo, que para una aplicación que incluía un láser Excimer no era un problema. Estrictamente hablando, puede haber topologías 2D que este modulador no pueda tratar en una sola imagen. No obstante, ASML decidió utilizar esta solución para su gigante de escritura directa. Lamentablemente, ASML nunca llegó a comercializar este producto. Que yo sepa, se trata de la mayor SLM diseñada y fabricada hasta la fecha. 11 millones de espejos de 8 micras de inclinación analógica y una velocidad de repetición de imagen de 6 kHz. Puede encontrar una bonita imagen Imagen SEM de la misma aquí.

Más información

Si quiere saber más, no dude en póngase en contacto conmigo a través de la página de contacto o simplemente enviando un correo electrónico a [email protected]. Me gusta hablar de los SLM. También puedes dejar un comentario aquí mismo.