Cartographie des distorsions - Un mode d'emploi de la SVD

Dans cet exposé technique, j'aimerais expliquer comment (et probablement comment ne pas) mettre au point une correction de la distorsion optique. Il s'agit d'une problème optique courantIl s'agit d'une aberration de front d'onde, qui peut être compensée par un algorithme, car même si l'image est déformée, elle peut toujours être exempte d'aberrations de front d'onde. Je suppose que le titre annonce déjà la couleur, il s'agira d'une suite à mon histoire d'amour avec la décomposition en valeurs singulières.

Ce problème est intéressant, non seulement parce qu'il est courant, mais aussi parce qu'il démontre clairement ce qu'est la SVD et ses forces innées. Avant de nous plonger dans les chiffres, replaçons le contexte.

Hypothèses sur le problème à résoudre

Dans le cas d'un système bien aligné présentant une distorsion importante, nous disposons d'une symétrie de rotation, et le polynôme radial sera le meilleur moyen de remédier à l'effet. Ce n'est cependant pas le problème qui m'intéresse. Le problème que j'aimerais aborder est celui où la distorsion est faible et où, lorsque nous la mesurons, nous ne pouvons pas ignorer le bruit de la mesure. Cependant, même si cette distorsion est faible, elle ne l'est pas suffisamment pour que nous puissions l'ignorer. Où pourrions-nous trouver une telle application ? Je pense que la lithographie est un exemple où nous pourrions chercher à la corriger à mieux qu'une partie sur cent mille. À ce niveau de précision, nous ne pouvons rien supposer sur la nature de la distorsion. L'optique est aussi bonne que possible et il y a toujours une distorsion que nous pouvons mesurer.

Le problème de la correction des distorsions s'inscrit bien dans le cadre de la SVD, car nous pouvons collecter des données qui s'adaptent au formalisme matriciel. Par conséquent, je supposerai que nous collecterons les informations de distorsion sur une grille qui couvre uniformément une image rectangulaire.

Sautons donc à pieds joints dans l'aventure. Voyons ce que nous pouvons attendre de cette approche. Pour générer des données de distorsion avec lesquelles nous pouvons expérimenter, j'ai écrit un script Matlab/Octave. Les lecteurs qui souhaitent l'expérimenter peuvent le télécharger ici. (Vous pouvez envoyer un courriel à contact pour y accéder si vous ne l'avez pas déjà)

N = 6 ;
[x,y] = meshgrid(-10:10, -13:13) ;
x = x/max(x( :)) ;
y = y/max(y( :)) ;
%a = randn(1,(N+1)*(N+2)/2).*(1 :((N+1)*(N+2)/2))/N^2 ;
fx = a(1)*x + a(2)*y + ...
      a(3)*x.^2 + a(4)*x.*y + a(5)*y.^2 + ...
      a(6)*x.^3 + a(7)*x.^2.*y + a(8)*x.*y.^2 + a(9)*y.^3 + ...
      a(10)*x.^4 + a(11)*x.^3.*y + a(12)*x.^2.*y.^2 + a(13)*x.*y.^3 + a(14)*y.^4 + ...
      a(15)*x.^5 + a(16)*x.^4.*y + a(17)*x.^3.*y.^2 + a(18)*x.^2.*y.^3 + a(19)*x.*y.^4 + a(20)*y.^5 ;
% a(20)*x.^6 + a(21)*x.^5.*y + a(22)*x.^4.*y.^2 + a(23)*x.^3.*y.^3 + a(24)*x.^2.*y.^4 + a(25)*x.*y.^5 + a(26)*y.^6 ;

%b = randn(1,(N+1)*(N+2)/2).*(1 :((N+1)*(N+2)/2))/N^2 ;
fy = b(1)*x + b(2)*y + ...
     b(3)*x.^2 + b(4)*x.*y + b(5)*y.^2 + ...
     b(6)*x.^3 + b(7)*x.^2.*y + b(8)*x.*y.^2 + b(9)*y.^3 + ...
     b(10)*x.^4 + b(11)*x.^3.*y + b(12)*x.^2.*y.^2 + b(13)*x.*y.^3 + b(14)*y.^4 + ...
     b(15)*x.^5 + b(16)*x.^4.*y + b(17)*x.^3.*y.^2 + b(18)*x.^2.*y.^3 + b(19)*x.*y.^4 + b(20)*y.^5 ;
% b(21)*x.^6 + b(22)*x.^5.*y + b(23)*x.^4.*y.^2 + b(24)*x.^3.*y.^3 + b(25)*x.^2.*y.^4 + b(26)*x.*y.^5 + a(27)*y.^6 ;

fx = fx + 1*randn(size(fx))/400 ;
fy = fy + 1*randn(size(fy))/400 ;
[ux,sx,vx] = svd(fx) ;
[uy,sy,vy] = svd(fy) ;

SVD et séparation des variables - une analogie

Le code ci-dessus est simplement une expansion de MacLaurin jusqu'au 5e ordre avec des coefficients aléatoires. L'expansion définit les déplacements le long de l'axe des coordonnées sur une grille que nous analysons à l'aide de la décomposition en valeurs singulières. Le résultat d'une analyse SVD est une décomposition matricielle qui divise la matrice en trois termes,

La matrice "S" est diagonale et (conventionnellement) triée par ordre décroissant. Les colonnes de la matrice U et V sont orthogonales et (généralement) normalisées,

Avant de nous plonger dans les détails de l'analyse de la distorsion de notre modèle, j'aimerais faire le lien entre l'UDS et quelque chose que la plupart des lecteurs connaissent peut-être déjà, la méthode de séparation des variables. Lorsque nous voulons résoudre une équation différentielle partielle de manière analytique, nous supposons que la solution peut être écrite sous la forme suivante,

Cela nous conduit ensuite à une solution que nous écrivons comme suit,

C'est exactement l'objectif de la décomposition en valeurs singulières. Elle permet d'écrire notre matrice M comme un produit de fonctions qui couvrent indépendamment l'espace des lignes et des colonnes de la matrice. Lorsque nous avons préparé nos entrées, nous avons fait quelque chose de similaire où nos "fonctions de base" étaient toutes sortes de combinaisons de puissances de x et des pouvoirs de y multipliée par un coefficient (aléatoire). L'analyse SVD a réduit notre ensemble de 20 fonctions d'entrée à deux ensembles (U et V) de 6 fonctions. Nous pouvons le constater en exécutant le script (une version complète du script peut être téléchargée). ici)

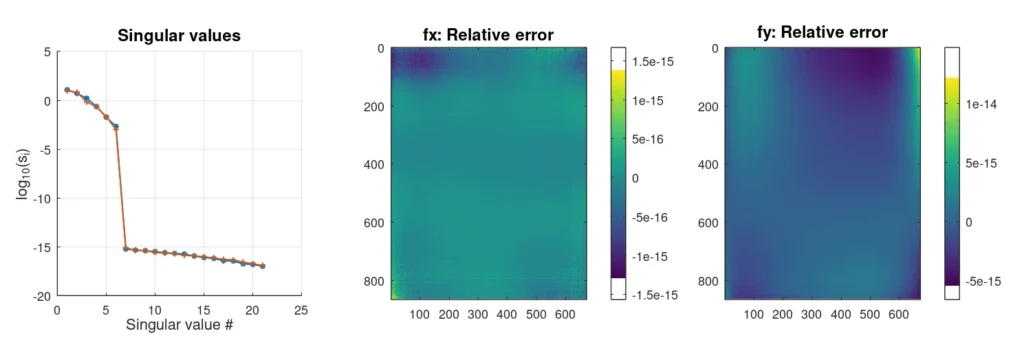
Les résultats ci-dessus ont été générés sans ajouter de bruit afin de séparer clairement ce qui est une solution et ce qui est (numériquement) zéro.

Analyse de la distorsion avec le bruit

Lorsque nous sommes confrontés à des données réelles, du moins pour les hypothèses que j'ai formulées ci-dessus, nous ne pouvons pas supposer que nous connaissons l'ampleur de notre expansion. C'est quelque chose que nous n'avons pas encore compris. Par conséquent, ajoutons un peu de bruit et voyons ce que cela donne,

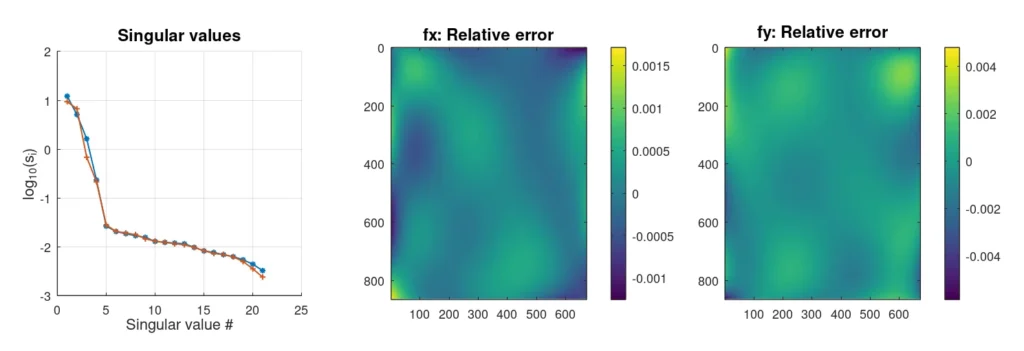
Avec l'ajout de bruit, la structure des valeurs singulières semble différente. Alors que dans le premier cas, les valeurs singulières chutaient de 12 ordres de grandeur après les 6 initiales, on observe maintenant ce qui ressemble à un croisement entre deux lignes droites. Ce phénomène est en fait assez courant lorsque l'on ajoute du bruit blanc. Pour notre modèle de distorsion, le bruit blanc est probablement une bonne hypothèse car les mesures devraient être indépendantes.

Le script nous montre également que notre récupération de la distorsion (échantillonnée 32×32 fois) n'est pas parfaite. Le bruit ne nous permet pas de récupérer de manière fiable plus de 5 composantes. Nous pourrions également nous demander si la cinquième composante est du bruit ou des données. En exécutant le script suffisamment de fois pour recueillir des statistiques, j'ai conclu que l'erreur était plus faible si l'on considérait qu'il s'agissait de données et qu'on les incluait. Ce qui est encore plus intéressant, c'est qu'en incluant ce cinquième point, la cartographie supprime les valeurs aberrantes qui apparaîtraient autrement 1,5% ou 2% des fois où nous avons réexécuté la simulation.

L'inclusion du 5e terme a une valeur très spécifique. Elle donne à la distribution des erreurs un aspect très gaussien. Selon nos yeux (ou nos cœurs) d'ingénieurs, cela devrait être très souhaitable. Les valeurs aberrantes peuvent être très coûteuses dans un contexte d'ingénierie, entraînant des retards et des frustrations. Pour clore le sujet, j'entends par valeur aberrante un événement dont la fréquence n'est pas prévue par les statistiques gaussiennes, comme une erreur de 6 écarts types se produisant une fois dans un échantillon de mille. De tels événements devraient nécessiter deux milliards d'échantillons.

Commentaires sur le texte

Il y a des choses dans la scénario qui méritent qu'on s'y attarde un peu. L'une des plus troublantes est que lorsque nous interpolons et rééchantillonnons les vecteurs singuliers gauche et droit (colonnes des matrices U et V), ils ne sont plus orthogonaux. Cela signifie que nous ne pouvons pas utiliser les vecteurs interpolés pour projeter d'autres distributions sur cet espace. Le manque d'orthogonalité ne semble cependant pas ajouter de biais à la reconstruction.

En outre, les interpolations utilisent le nombre de valeurs singulières extraites comme ordre du polynôme utilisé pour l'interpolation. Il est facile d'argumenter en faveur de ce choix pour un modèle comme celui-ci. Ce choix, cependant, serait l'un des premiers que j'essaierais de confirmer (ou de rejeter) lorsque je serais confronté à des données réelles.

Si vous avez trouvé cela intéressant, veuillez laisser un commentaire. Cela ne me dérangerait pas de réécrire ce programme en C open-source et d'inclure le pré-gauchissement des données d'entrée. Il y a aussi des considérations numériques très intéressantes sur la façon de structurer les données pour qu'une application de cette théorie puisse traiter des taux de mappage de giga pixels par seconde, ce qui semble être réalisable avec des CPU génériques.

Merci de votre lecture.