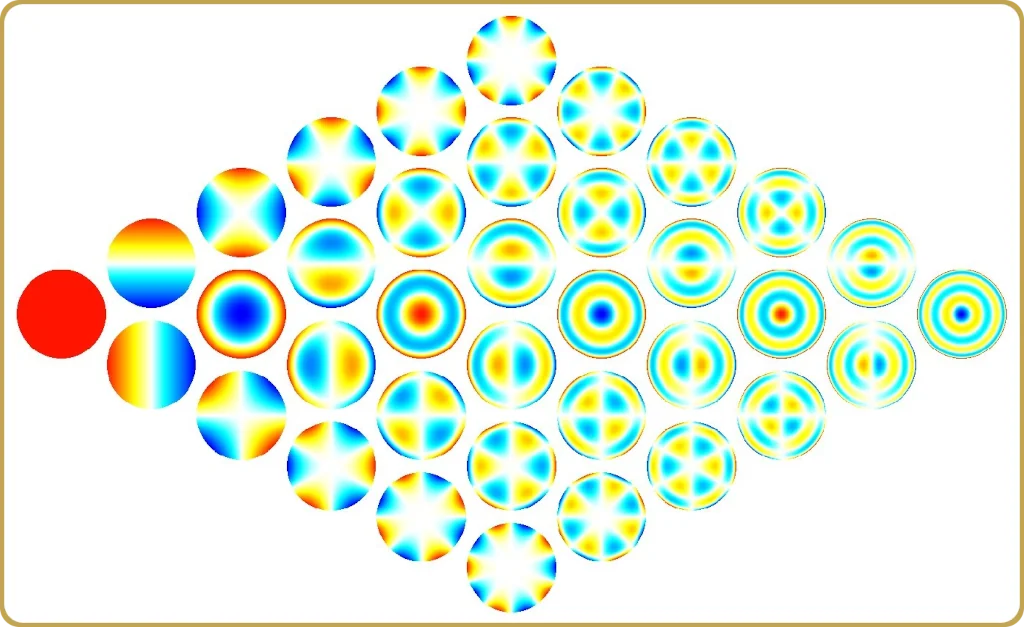
Les polynômes de Zernike, nous les reconnaissons tous et ils constituent le langage que nous utilisons souvent pour décrire les systèmes optiques. Mais est-ce toujours le bon langage ?
Y a-t-il une mauvaise langue ? En fin de compte, nous essaierions de pousser une conception à zéro pour qu'elle n'ait pas d'importance. Mais bon, zéro, ce serait comme ne rien dire.
Que se passe-t-il si nous ne pouvons pas atteindre zéro ou si, dans le cadre de la tolérance, nous pouvons choisir de pousser tel ou tel terme, mais pas les deux. Comment choisir ? Si nous fabriquons un télescope, la situation est claire. Nous voulons minimiser la variance du front d'onde et, par conséquent, maximiser le rapport de Strehl. Born et Wolf l'expliquent très clairement.
Mais qu'en est-il si la propriété qui nous intéresse n'est pas dérivée de la variance ? Comment le savoir ?
Une analyse qui peut être employée consiste à trouver l'expansion de MacLaurin de la propriété d'intérêt au second ordre en utilisant le polynôme de Zernike comme (disons) sondes ou simplement comme paramètres libres. Pour ce faire, on peut utiliser une approche de Monte Carlo ou une approche d'échantillonnage d'hypercubes latins, et le choix de la meilleure approche fera l'objet d'une autre discussion. Cependant, une fois que nous avons fait cela, nous pouvons trouver le c, le v et le A qui correspondent le mieux aux données, et cette correspondance peut être vraiment très bonne.
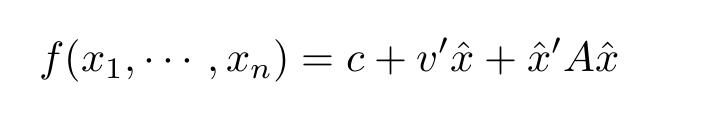
Si A n'est pas diagonale dans cette expansion, les polynômes de Zernike ne sont pas le bon langage car il ne s'ensuit pas que la minimisation de l'un des coefficients améliore toujours la propriété qui nous intéresse. Dans ce cas, la diagonalisation des A nous donnera une nouvelle base orthogonale.
Cependant, avant de poser la question des termes à minimiser, mais dans la nouvelle base, qu'en est-il du terme linéaire v. La réponse à cette question est : cela dépend. Il y a évidemment la possibilité de chercher la solution au problème de la f = 0 et si cette solution se situe dans le domaine de validité de l'expansion, nous avons probablement trouvé une solution non triviale où des aberrations non nulles génèrent une erreur nulle. Cela arrive, mais très souvent, soit v est essentiellement nulle ou la solution de f = 0 ne se situe pas dans le champ d'application de l'expansion.
Lorsque le terme linéaire v est égal à zéro, nous nous posons alors la même question qu'au départ : devons-nous améliorer tel ou tel terme dans la nouvelle base ? La réponse est la suivante : cela n'a pas d'importance, car tant que nous réduisons la somme incohérente (en quadrature) de ces termes, la propriété qui nous intéresse s'améliore.
C'est sans doute un peu ésotérique, mais si nous disposons des modèles de notre système optique et de la propriété qui nous intéresse, il est tout à fait possible de sonder 15 à 20 paramètres libres à l'aide de quelques milliers de simulations et d'obtenir des informations précieuses sur les principes fondamentaux du système optique. Souvent, cela peut être fait en moins d'une journée si nous avons déjà les modèles en place.





Laisser un commentaire