Verzerrungsabbildung - Ein SVD HowTo

In diesem Tech-Talk möchte ich erörtern, wie man eine optische Verzeichnungskorrektur entwickelt (und wahrscheinlich auch, wie man sie nicht entwickelt). Es ist eine gemeinsames optisches Problemund eine, die tatsächlich mit einem Algorithmus kompensiert werden kann, denn selbst wenn das Bild verzerrt ist, kann es immer noch frei von Wellenfrontaberrationen sein. Ich schätze, der Titel verrät es schon, es wird eine Fortsetzung meiner Liebesgeschichte mit der Singulärwertzerlegung sein.

Dieses Problem ist nicht nur interessant, weil es häufig vorkommt, sondern auch, weil es so deutlich zeigt, was die SVD ist und welche Stärken sie hat. Bevor wir uns nun mit einigen Zahlen beschäftigen, sollten wir zunächst den Kontext herstellen.

Annahmen über das zu lösende Problem

Bei einem gut ausgerichteten System mit einer großen konstruktionsbedingten Verzerrung haben wir Rotationssymmetrie, und ein radiales Polynom ist die beste Lösung für diesen Effekt. Dies ist jedoch nicht das Problem, an dem ich interessiert bin. Das Problem, mit dem ich mich befassen möchte, ist ein Problem, bei dem die Verzerrung klein ist, und wenn wir sie messen, können wir das Messrauschen nicht ignorieren. Aber selbst wenn die Verzerrung klein ist, ist sie nicht so klein, dass wir sie ignorieren könnten. Wo könnten wir eine solche Anwendung finden? Ich denke, die Lithografie ist ein Beispiel, bei dem wir eine Korrektur von mehr als einem Teil unter hunderttausend anstreben können. Bei diesem Genauigkeitsgrad können wir nichts über die Art der Verzerrung annehmen. Die Optik ist so gut wie möglich, und es gibt immer noch eine Verzerrung, die wir messen können.

Das Problem der Verzerrungskorrektur passt gut in den SVD-Rahmen, da wir Daten sammeln können, die in den Matrixformalismus passen. Daher gehe ich davon aus, dass wir die Verzerrungsinformationen auf einem Gitter sammeln, das gleichmäßig ein rechteckiges Bild abdeckt.

Steigen wir also gleich mit beiden Füßen ein. Schauen wir uns an, was wir von diesem Ansatz erwarten können. Um einige Verzerrungsdaten zu erzeugen, mit denen wir experimentieren können, habe ich ein Matlab/Octave-Skript geschrieben. Leser, die damit experimentieren möchten, können es herunterladen hier. (Sie können eine E-Mail senden an Kontakt um Zugang zu erhalten, wenn Sie ihn noch nicht haben)

N = 6;
[x,y] = meshgrid(-10:10, -13:13);
x = x/max(x(:));
y = y/max(y(:));
%a = randn(1,(N+1)*(N+2)/2).*(1:((N+1)*(N+2)/2))/N^2;
fx = a(1)*x + a(2)*y + ...
      a(3)*x.^2 + a(4)*x.*y + a(5)*y.^2 + ...
      a(6)*x.^3 + a(7)*x.^2.*y + a(8)*x.*y.^2 + a(9)*y.^3 + ...
      a(10)*x.^4 + a(11)*x.^3.*y + a(12)*x.^2.*y.^2 + a(13)*x.*y.^3 + a(14)*y.^4 + ...
      a(15)*x.^5 + a(16)*x.^4.*y + a(17)*x.^3.*y.^2 + a(18)*x.^2.*y.^3 + a(19)*x.*y.^4 + a(20)*y.^5 ;
% a(20)*x.^6 + a(21)*x.^5.*y + a(22)*x.^4.*y.^2 + a(23)*x.^3.*y.^3 + a(24)*x.^2.*y.^4 + a(25)*x.*y.^5 + a(26)*y.^6;

%b = randn(1,(N+1)*(N+2)/2).*(1:((N+1)*(N+2)/2))/N^2;
fy = b(1)*x + b(2)*y + ...
     b(3)*x.^2 + b(4)*x.*y + b(5)*y.^2 + ...
     b(6)*x.^3 + b(7)*x.^2.*y + b(8)*x.*y.^2 + b(9)*y.^3 + ...
     b(10)*x.^4 + b(11)*x.^3.*y + b(12)*x.^2.*y.^2 + b(13)*x.*y.^3 + b(14)*y.^4 + ...
     b(15)*x.^5 + b(16)*x.^4.*y + b(17)*x.^3.*y.^2 + b(18)*x.^2.*y.^3 + b(19)*x.*y.^4 + b(20)*y.^5;
% b(21)*x.^6 + b(22)*x.^5.*y + b(23)*x.^4.*y.^2 + b(24)*x.^3.*y.^3 + b(25)*x.^2.*y.^4 + b(26)*x.*y.^5 + a(27)*y.^6;

fx = fx + 1*randn(size(fx))/400;
fy = fy + 1*randn(size(fy))/400;
[ux,sx,vx] = svd(fx);
[uy,sy,vy] = svd(fy);

SVD und Variablentrennung - eine Analogie

Der obige Code ist lediglich eine MacLaurin-Erweiterung bis zur 5. Ordnung mit Zufallskoeffizienten. Die Expansion definiert Verschiebungen entlang der Koordinatenachse über ein Gitter, das wir mit Hilfe der Singulärwertzerlegung analysieren. Das Ergebnis einer SVD-Analyse ist eine Matrixzerlegung, bei der die Matrix in drei Terme zerlegt wird,

Die Matrix "S" ist diagonal und (konventionell) in absteigender Reihenfolge sortiert. Die Spalten der U und V Matrizen sind orthogonal und (normalerweise) normalisiert,

Bevor wir in die Details der Analyse unserer Modellverzerrung eintauchen, möchte ich die SVD mit etwas in Verbindung bringen, mit dem die meisten Leser vielleicht schon vertraut sind, nämlich mit der Methode der Trennung von Variablen. Wenn wir eine partielle Differentialgleichung analytisch lösen wollen, gehen wir davon aus, dass die Lösung wie folgt geschrieben werden kann,

Dies führt uns später zu einer Lösung, die wir wie folgt schreiben,

Genau das ist der Zweck der Singulärwertzerlegung. Sie bietet eine Möglichkeit, unsere Matrix zu schreiben M als ein Produkt von Funktionen, die unabhängig voneinander den Zeilen- und Spaltenraum der Matrix abdecken. Als wir unsere Eingaben vorbereitet haben, haben wir etwas Ähnliches gemacht, wobei unsere "Basisfunktionen" alle möglichen Kombinationen von Potenzen von x und Befugnisse von y multipliziert mit einem (zufälligen) Koeffizienten. Die SVD-Analyse hat unsere Menge von 20 Eingabefunktionen auf zwei Mengen (U und V) von 6 Funktionen reduziert. Wir können dies sehen, indem wir das Skript ausführen (eine vollständige Version des Skripts kann heruntergeladen werden hier)

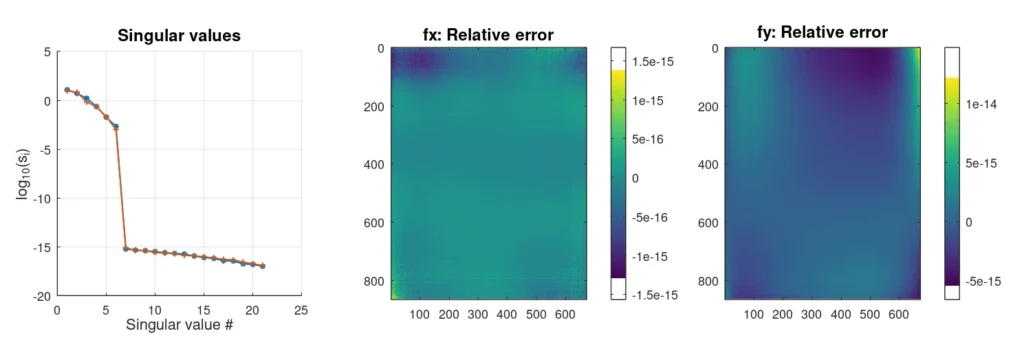
Die obigen Ergebnisse wurden ohne Hinzufügen von Rauschen erzeugt, um sauber zu trennen, was eine Lösung ist und was (numerisch) Null ist.

Analyse der Verzerrung durch Rauschen

Wenn wir mit realen Daten konfrontiert werden, können wir - zumindest bei den Annahmen, die ich oben gemacht habe - nicht davon ausgehen, dass wir den Umfang unserer Expansion kennen. Das ist etwas, das wir noch herausfinden müssen. Fügen wir also etwas Rauschen hinzu und sehen wir, wie es aussieht,

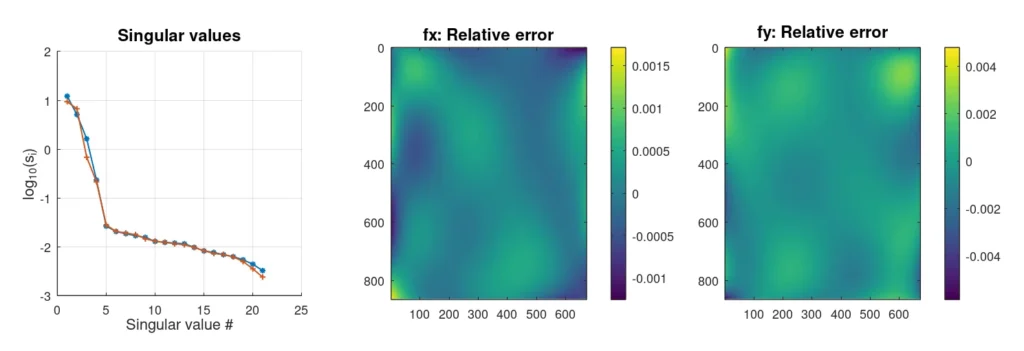
Mit dem hinzugefügten Rauschen sieht die Struktur der Singulärwerte anders aus. Während im ersten Fall die Singulärwerte nach den anfänglichen 6 um 12 Größenordnungen abfielen, gibt es jetzt etwas, das wie eine Kreuzung zwischen zwei geraden Linien aussieht. Dies ist eigentlich ganz normal, wenn wir weißes Rauschen hinzufügen. Für unser Verzerrungsmodell ist weißes Rauschen wahrscheinlich eine gute Annahme, da die Messungen unabhängig sein sollten.

Das Skript zeigt uns nun auch, dass unsere Wiederherstellung der Verzerrung (32×32-faches Up-Sampling) nicht perfekt ist. Das Rauschen erlaubt es uns nicht, mehr als 5 Komponenten zuverlässig wiederherzustellen. Wir könnten auch darüber streiten, ob es sich bei der 5. Komponente um Rauschen oder um Daten handelt. Nachdem ich das Skript oft genug ausgeführt hatte, um einige statistische Daten zu sammeln, kam ich zu dem Schluss, dass der Fehler geringer ist, wenn wir sie als Daten betrachten und einbeziehen. Noch wertvoller ist die Tatsache, dass durch die Einbeziehung dieses 5. Punktes die Abbildung Ausreißer unterdrückt, die sonst 1,5% oder 2% der Male, die wir die Simulation erneut ausführen, auftreten würden.

Die Einbeziehung des 5. Terms hat einen sehr spezifischen Wert. Er lässt die Fehlerverteilung ziemlich gaußförmig aussehen. In den Augen (oder Herzen) unserer Ingenieure sollte dies sehr wünschenswert sein. Ausreißer können in einem technischen Kontext sehr kostspielig sein und zu Verzögerungen und Frustration führen. Um das Thema abzuschließen: Mit Ausreißer meine ich ein Ereignis, dessen Häufigkeit von der Gaußschen Statistik nicht vorhergesagt wird, z. B. ein Fehler von 6 Standardabweichungen, der einmal in einer Stichprobe von Tausend auftritt. Für solche Ereignisse sollten zwei Milliarden Stichproben erforderlich sein.

Kommentare zum Drehbuch

Es gibt einige Dinge in der Skript die es wert sein könnten, ein wenig darüber nachzudenken. Am beunruhigendsten finde ich, dass die linken und rechten singulären Vektoren (Spalten der U- und V-Matrizen) nicht mehr orthogonal sind, wenn wir sie interpolieren und neu abtasten. Das bedeutet, dass wir die interpolierten Vektoren nicht für die Projektion anderer Verteilungen auf diesen Raum verwenden können. Das Fehlen der Orthogonalität scheint die Rekonstruktion jedoch nicht zu verfälschen.

Außerdem verwenden die Interpolationen die Anzahl der extrahierten Singulärwerte als Ordnung des für die Interpolation verwendeten Polynoms. Es ist leicht, für diese Wahl bei einem Modell wie diesem zu argumentieren. Diese Wahl wäre jedoch eine der ersten, die ich versuchen würde zu bestätigen (oder zu verwerfen), wenn ich mit echten Daten konfrontiert würde.

Wenn Sie dies interessant finden, hinterlassen Sie bitte einen Kommentar. Ich hätte nichts dagegen, dies in ein Open-Source-C-Programm umzuschreiben und eine Vorverzerrung der Eingabedaten einzubauen. Es gibt auch einige recht interessante numerische Überlegungen, wie man die Daten strukturieren kann, um eine Anwendung dieser Theorie in die Lage zu versetzen, Abbildungsraten von Giga-Pixeln pro Sekunde zu bewältigen, was mit generischen CPUs erreichbar zu sein scheint.

Vielen Dank für die Lektüre.