Concevoir de nouveaux systèmes optiques à partir de la base peut être une tâche intimidante, surtout si le système que nous essayons de créer doit être parfait avant de pouvoir être construit parce que les composants critiques n'existent tout simplement pas encore. Il s'agit simplement d'un fruit de notre imagination et c'est en fait une partie de notre tâche que de le définir. Des situations similaires se présenteront lorsque nous explorerons différentes conceptions et que nous voudrons apprendre comment les choses fonctionnent réellement avant d'entreprendre la tâche de les construire.
Imaginons la situation. Vous devez trouver les exigences d'un système que nous n'avons jamais étudié auparavant et s'il existe un article scientifique qui pourrait être lié à ce dont nous avons besoin, allons-nous seulement le trouver ? Il n'est pas rare que nous réinventions la roue. Dirac a réinventé l'algèbre de Clifford lorsqu'il a dérivé les équations quantiques pour l'électron. Partons donc du principe que, de toute façon, c'est à nous qu'incombe la responsabilité.
La stratégie à adopter à ce stade consisterait à élaborer un modèle - une sorte de carte, mais pas n'importe laquelle ; elle doit être suffisamment détaillée pour permettre de naviguer dans tous les méandres essentiels (lire : degrés de liberté), sans pour autant être trop complexe pour que l'on ne voie pas la forêt dans les arbres. C'est là que réside notre premier défi : à moins que cette machine ne soit un proche cousin d'une machine que nous maîtrisons déjà, notre carte tient plus de la conjecture que de l'évangile. Nous ne savons pas très bien quels chemins (degrés de liberté) sont les plus importants et quels sont ceux qui ne sont que des détails.
Sans la bonne boussole (les bons outils) pour naviguer dans la complexité, nous risquons de simplifier à l'extrême notre carte, limités davantage par notre imagination que par le terrain réel.
Réduire la complexité
L'un des moyens de résoudre ce problème, que j'ai trouvé efficace, consiste à utiliser une expansion mathématique bien connue autour de l'état idéal du système étudié, essentiellement une expansion de Maclaurin. Puisque l'outil que nous recherchons est celui qui libère notre analyse de nos propres limites mentales, il doit nous permettre de sonder notre système avec un grand nombre de variables indépendantes.
Il existe différentes façons d'aborder cette question, mais l'une d'entre elles, que j'ai trouvée très efficace, est ce que l'on appelle l'échantillonnage par hypercubes latins (LHS), que l'on appelle aussi parfois un plan de remplissage de l'espace.
La génération d'un LHS prend un certain temps, mais dans la plupart des cas, cela prend moins de quelques minutes, même si le nombre de variables indépendantes est élevé. Le temps nécessaire à la génération d'un LHS croît linéairement avec le nombre de variables et à la puissance 3 avec le nombre d'échantillons. Heureusement, il ne s'agit que d'une complexité polynomiale, ou "facile" si l'on s'adresse aux spécialistes de la complexité informatique.
Un exemple de cas où un grand nombre de DOF peut être intéressant est celui où l'on veut dériver une spécification pour un système optique et où les DOF sont les coefficients polynomiaux de Zernike.
La LHS nous donne un ensemble d'échantillons uniformément distribués dans un espace multidimensionnel, mais il nous appartient toujours de poser la bonne question et, dans ce cas, il n'y a pratiquement pas de mauvaise question.
Ainsi, par exemple, en utilisant cet ensemble d'échantillons, on peut mettre en place un ensemble de simulations qui sondent la variance de la propriété, ou nous pouvons simuler comment une propriété déterministe dépend de notre DOF. Les deux peuvent être très utiles, mais avant d'approfondir cette question, voyons comment obtenir des résultats à analyser.
Second order exapansion
Aussi simple que cela puisse paraître, il s'agit d'une approche très précieuse qui offre des aperçus qui se transforment souvent en moments d'émerveillement.
En utilisant ces points d'échantillonnage dans notre problème multidimensionnel, nous effectuons un nombre égal de simulations afin d'obtenir un résultat numérique pour chacun d'entre eux. Cependant, tout cela n'est pas très instructif. Nous devons réduire cette complexité. Nous devons résumer toutes ces simulations, qui pourraient facilement se chiffrer à plusieurs milliers, en quelque chose que nous pouvons saisir, quelque chose qui trie l'ivraie du bon grain, pour ainsi dire.
Pour ce faire, nous essayons d'exprimer nos résultats à l'aide d'une expansion du second ordre,
Cela ressemble beaucoup à la façon dont nous exprimerions un développement de MacLaurin, mais le fait est que le gradient et le Hessien sont toujours inconnus et que nous devons les trouver. Pouvons-nous le faire ?
Oui, nous le pouvons. Nous disposons de nombreuses informations et trouver le coefficient de v et H est un problème linéaire. Pour un 2 DOF, nous avons 1 inconnue "c", deux inconnues dans le terme linéaire "v" et 2 + 1 dans "H" parce que H est symétrique. Pour 3 DOF, nous avons 1 + 3 + 3 + 2 + 1 et ainsi de suite. Il s'agit simplement d'algèbre linéaire. Nos milliers de simulations et le pseudo-inverse de More Penrose nous donneront ces inconnues plus vite que nous ne pouvons dire "solution numérique".
Vers les bonnes choses
C'est maintenant que les choses intéressantes commencent. En supposant que nos expansions du deuxième ordre sont bonnes, nous avons réduit des milliers de simulations en un modèle que nous pouvons maintenant commencer à décortiquer davantage.
La première chose que l'on fait généralement après avoir obtenu l'extension est de vérifier dans quelle mesure cette extension reproduit les milliers de résultats simulés. Très souvent, la corrélation entre le modèle et les simulations est supérieure à 99 %. Je considérerais que 95 % est à peine utile, mais le résultat habituel se situe autour de 99 % ou mieux. Cela dépendra bien sûr de la nature de la propriété sous-jacente, si notre modèle numérique concerne une propriété statistique ou non.
Avant d'avoir joué avec ce modèle, nous ne le savons pas, mais je n'ai pas encore trouvé de cas qui ne pourrait pas être transformé d'une manière ou d'une autre pour permettre à cette expansion de capturer essentiellement toute la variance de nos simulations.
Analyse de l'expansion
Nous arrivons maintenant à la partie où nous pouvons récolter les fruits de notre dur labeur. Il y a typiquement trois types de résultats, soit l'expansion est dominée par le terme linéaire, soit par le terme carré, soit elle est mixte, ce qui est en fait assez intéressant car cela nous indique que notre expansion n'est pas autour d'un minimum.
Si le terme linéaire domine, je suppose que c'est tout. Il n'y a pas d'interactions entre les DOF. L'affaire est close. Notre système était simple, et si nous ne l'avions pas compris avant, nous le comprenons certainement maintenant.
La situation devient plus intéressante lorsque le terme du second ordre domine l'expansion, car il y a alors plus à apprendre. Ce qu'il faut faire ici, c'est certainement faire appel à l'algèbre linéaire et réécrire H comme suit,
à l'aide de la décomposition en valeurs singulières (SVD).
Si vous êtes arrivé jusqu'ici et que vous choisissez de ne pas saisir cette opportunité, cela équivaudrait à ce que Néo prenne la pilule bleue, choisisse de dormir et de croire ce qu'il veut croire. Ne prenez jamais la pilule bleue.
Si votre système doit être exprimé en termes de matrice du second ordre, vous devez rester au pays des merveilles et laisser la SVD vous montrer la profondeur du trou de la souris.
Il ne s'agit pas seulement d'un jeu de chiffres théorique. Vous pouvez avoir besoin de le savoir lors de la conception de vos optiques car, non seulement cela vous indique que certaines combinaisons d'aberrations doivent être optimisées ensemble, mais les éléments diagonaux de Σ vous indiquent également l'importance réelle de chacune de ces combinaisons, ce qui constitue un indice inestimable de ce que la fonction de mérite doit supprimer le plus.
Qu'en est-il du cas mixte, où la partie linéaire et la partie carrée contribuent toutes deux de manière significative au modèle ? Ce cas est vraiment intéressant car il nous indique que, contrairement à ce que nous pensions initialement, le système n'a pas été étendu autour de l'état idéal.
Ce cas nécessite un peu de prudence car la solution dépend du modèle et, même dans ce cas, elle peut indiquer un nouveau minumum i en dehors du volume sondé par l'ensemble initial de points d'échantillonnage. Il se peut que la solution soit correcte, mais elle ne peut pas être considérée comme acquise.
C'est l'heure de l'exemple
Supposons que nous appliquions cette théorie à quelque chose comme le couplage de fibres. En restant dans l'esprit que nous ne savons pas comment cela fonctionne, nous utilisons les polynômes de Zernike comme degrés de liberté et, comme fonction de test, nous calculons la perte d'insertion en fonction de nos degrés de liberté.
Tout d'abord, nous devons définir le nombre de DOF que nous souhaitons étudier. Disons que nous nous arrêtons à Z16. Nous savons que Z1 n'a généralement pas d'importance, mais que ceux qui suivent en ont, donc 15 DOF.
Ensuite, nous générons 1024 points d'échantillonnage sur 15 DOF à l'aide du LHS. Le LHS génère généralement des points d'échantillonnage sur un hypercube, nous devons donc mettre ces valeurs à l'échelle de manière raisonnable. Si nous ne connaissons rien du sujet, nous devrions probablement commencer petit, vraiment petit. Ensuite, nous pouvons répéter le processus jusqu'à ce que nous trouvions que le modèle que nous calculons ne correspond plus très bien aux données ou jusqu'à ce que nous atteignions une gamme de valeurs que nous pensons être pertinentes pour notre système.
Maintenant, nous sautons un peu dans le temps et 1024 simulations de perte d'insertion plus tard, nous avons notre fonction f(x,....) et quelque chose à modéliser.(Cette simulation a supposé une apodisation de 2 et un mode fondamental gaussien. Ce blog n'est pas vraiment consacré aux fibres monomodes, alors pardonnez les hypothèses simplifiées sur les fibres monomodes).
Une fois que nous avons trouvé les coefficients de c, v et H, nous pouvons voir comment le modèle a rendu compte de nos simulations,
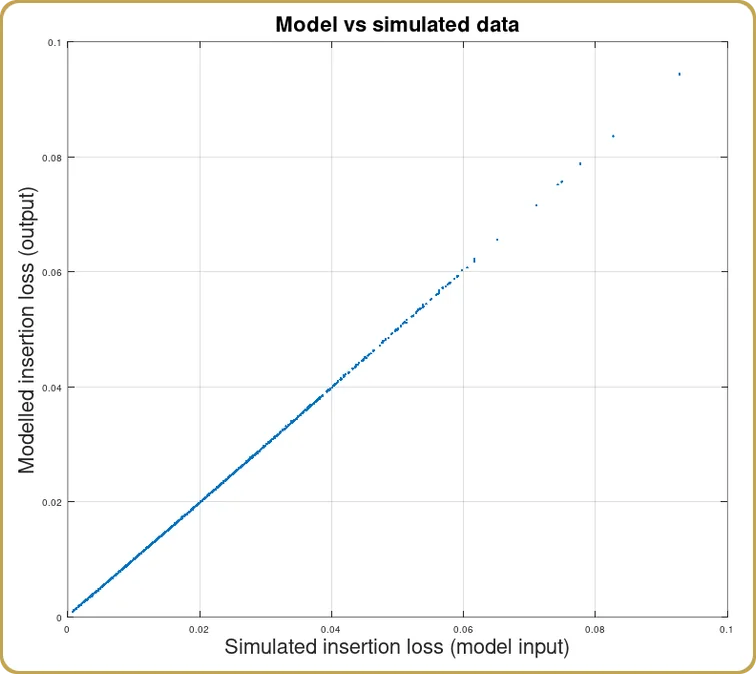
Comme prévu, nous avons obtenu une bonne corrélation entre les simulations et l'expansion du modèle. Étant donné que l'optique physique n'est décrite que par l'intégrale de recouvrement, il fallait s'y attendre. Après tout, il s'agit d'un exemple dont on peut s'inspirer.
Nous pouvons également examiner dans quelle mesure cette corrélation est due au terme linéaire,
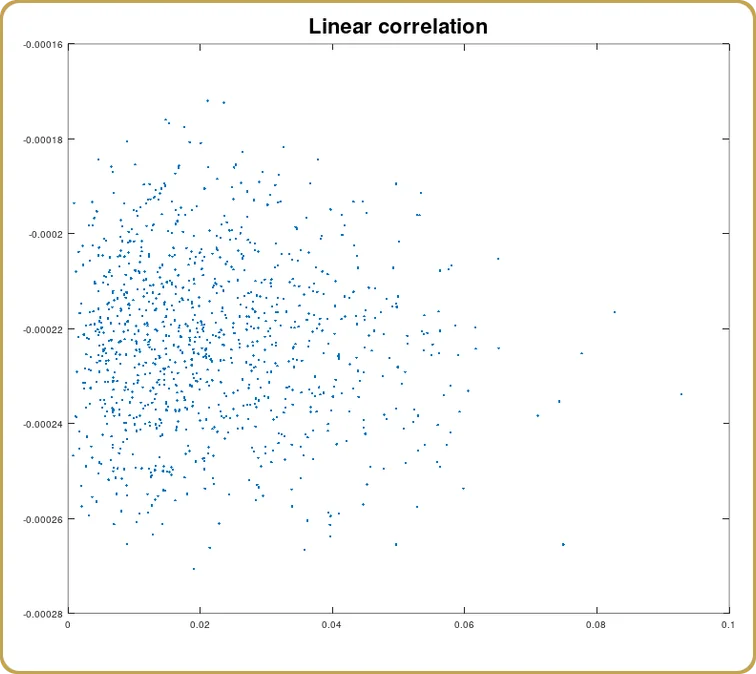
Et comme prévu, la corrélation est nulle (statistiquement). Nous avons modélisé quelque chose qui a un minimum à zéro aberration. La partie linéaire devrait disparaître. Examinons maintenant le terme carré.
J'espère qu'il est maintenant évident que nous allons utiliser la décomposition en valeurs singulières, vous vous souvenez de la pilule rouge, n'est-ce pas ? Nous lançons donc notre H dans la SVD et la première chose à examiner est la valeur singulière,
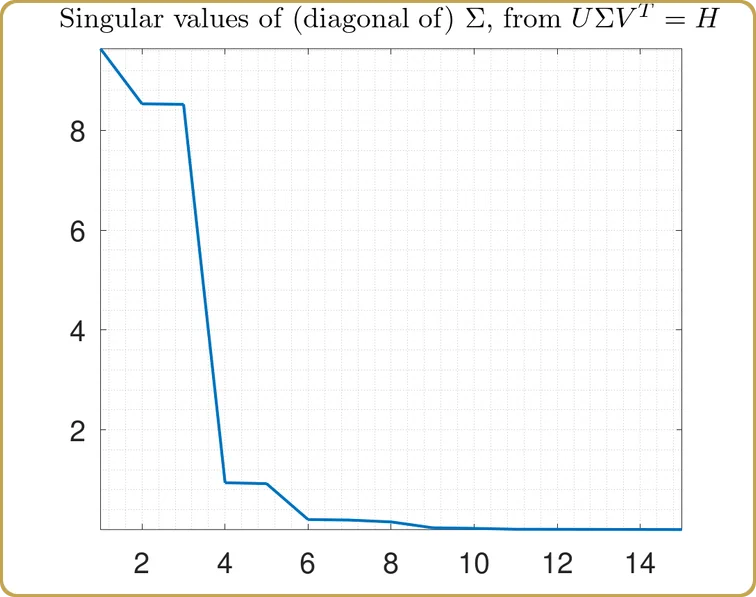
Les valeurs réelles sur l'axe des ordonnées ne sont pas si intéressantes, après tout, elles dépendent du volume de notre hypercube de test que nous avons utilisé pour échantillonner notre problème. Ce qui est plus intéressant, c'est la structure. Notre problème a été réduit à presque trois variables indépendantes, plus deux autres beaucoup moins importantes. Jetons un coup d'œil,
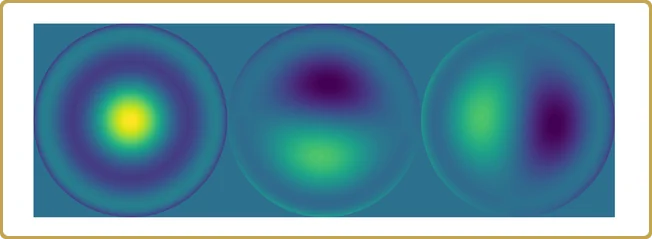
Il est temps de résumer.
Nous avons commencé avec 1024 valeurs simulées sur 15 dimensions d'un sujet dont nous ne connaissions (prétendument) rien et nous avons obtenu 3 contributions majeures à une propriété que nous voulions comprendre.
Il ne s'agit pas d'un résultat inhabituel dans ce type d'analyse. La corrélation n'est peut-être pas aussi bonne que dans cet exemple construit, mais avec une certaine transformation des données, le modèle de second ordre peut capturer essentiellement toute la variance de la simulation.
L'aspect le plus précieux de ce type d'analyse est peut-être le fait que nous pouvons prendre en compte un nombre beaucoup plus important de degrés de liberté et ne pas nous limiter à notre capacité à démêler la complexité ou, pour reprendre la métaphore de la carte, il n'y a pas d'arbres. Nous ne voyons que des bois et des collines. De ce point de vue, la vue d'ensemble est tout ce qu'il y a, et tout ce que nous avons payé pour cela, c'est du temps d'ordinateur.
Laisser une réponse