L'IA peut-elle faire votre code ?

Je crois que je suis en mission, une mission visant à modérer la crainte que les gens semblent éprouver à l'égard de l'IA.

Comme je travaille dans le domaine de l'optique, j'écris beaucoup de code, toutes sortes de code, et je souhaite évidemment passer le moins de temps possible à le faire.

Avant d'ajouter le tracé de Zernike utilisant le pipeline OpenGL à ma propre plateforme, j'ai demandé à ChatGPT d'en écrire un pour moi. C'était il y a 18 mois.
Inutile de dire que j'ai trouvé le résultat inutile. Pourquoi ? Encore une fois, comme dans mon post précédent, le code semblait correct à distance, mais dans les détails, il était inutile. Laissez-moi vous montrer ce que je veux dire.

Calcul des polynômes de Zernike

Lorsque vous calculez les polynômes de Zernike, vous devez calculer le polynôme radial (qui a pour paramètre la distance au centre pour une coordonnée donnée par x et y) et le sinus ou le cosinus de l'angle. Alors, laissez-moi vous demander, à vous les humains qui ne pouvez pas rivaliser avec l'IA jagernaut, si vous avez déjà calculé la distance (l'hypoténuse d'un triangle) en utilisant les coordonnées x et y, comment procédez-vous pour calculer le sinus et le cosinus de l'angle ?

Je pense que 100% d'entre vous qui avez lu jusqu'ici le font en divisant les x et les y par l'hypoténuse. Qu'est-ce que l'hypoténuse ? l'IA la plus récente et la plus performante faire ? Il prend les coordonnées et calcule l'angle en utilisant l'inverse de la tangente et, comme vous l'avez peut-être deviné, il utilise ensuite l'angle pour calculer le sinus et le cosinus.

Toute cette énergie pour quoi faire ?

C'est le résultat que j'ai vu il y a 18 mois, et 300 GWh (pour les seuls GPU, puis ajouter le refroidissement, le réseau), ou 90 jours d'apprentissage par renforcement plus tard et nous avons exactement le même résultat.

Il y a à peine un soupçon d'intelligence ici. Il s'agit simplement d'une traduction purement textuelle d'un manuel dans une autre forme de texte.

J'ai essayé d'attirer l'attention sur les rendements logarithmiques des performances de l'IA par rapport à la puissance de calcul. Dans ces conditions, j'opterais pour un rendement logarithmique à tout moment, car je ne vois aucune amélioration.

Évidemment, j'ai posé la même question à DeepSeek, et en fait (je plaisante), le résultat a été encore pire. Pas de beaucoup, car il est difficile de produire un code pire que celui-ci.

Si vous voulez tester par vous-même, voici mon invitation :
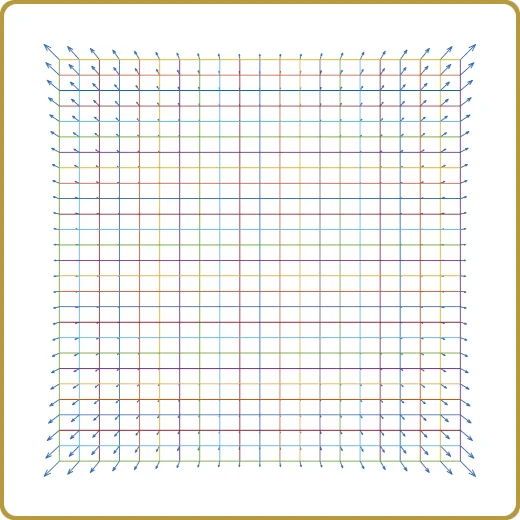
Pouvez-vous écrire un shader OpenGL qui génère une carte de densité 2D basée sur un vecteur de coefficients de Zernike ? Le résultat est illustré ci-dessous.

uniform vec2 resolution;         // Screen resolution
uniform float zernikeCoeffs[15]; // Array of Zernike coefficients (adjust size as needed)
uniform float scale;             // Scaling factor for the density map

// Convert cartesian (x,y) to polar (rho, theta)
vec2 cartesianToPolar(vec2 xy) {
    float rho = length(xy);
    float theta = atan(xy.y, xy.x);
    return vec2(rho, theta);
}

// Zernike radial polynomial function
float radialPoly(int n, int m, float rho) {
    float result = 0.0;
    m = abs(m);
    
    if ((n - m) % 2 != 0) return 0.0;
    
    for (int k = 0; k <= (n - m) / 2; k++) {
        float coef = 1.0;
        // Calculate binomial coefficient
        for (int i = 1; i <= k; i++) {
            coef *= float(n - 2 * k + i) / float(i);
        }
        for (int i = 1; i <= (n - m) / 2 - k; i++) {
            coef *= float(m + i) / float(i);
        }
        result += pow(-1.0, float(k)) * coef * pow(rho, float(n - 2 * k));
    }
    return result;
}

// Zernike polynomial evaluation
float zernike(int index, vec2 polar) {
    float rho = polar.x;
    float theta = polar.y;
    
    // Zernike polynomial ordering (n,m): (0,0), (1,-1), (1,1), (2,-2), (2,0), etc.
    int n, m;
    if (index == 0) { n = 0; m = 0; }    // Z0,0
    else if (index == 1) { n = 1; m = -1; } // Z1,-1
    else if (index == 2) { n = 1; m = 1; }  // Z1,1
    else if (index == 3) { n = 2; m = -2; } // Z2,-2
    else if (index == 4) { n = 2; m = 0; }  // Z2,0
    else if (index == 5) { n = 2; m = 2; }  // Z2,2
    else if (index == 6) { n = 3; m = -3; } // Z3,-3
    else if (index == 7) { n = 3; m = -1; } // Z3,-1
    else if (index == 8) { n = 3; m = 1; }  // Z3,1
    else if (index == 9) { n = 3; m = 3; }  // Z3,3
    else return 0.0;

    if (rho > 1.0) return 0.0;  // Zernike defined only within unit disk
    
    float radial = radialPoly(n, m, rho);
    if (m < 0) return radial * sin(float(-m) * theta);
    else return radial * cos(float(m) * theta);
}

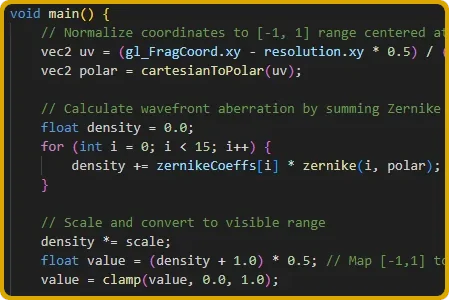
void main() {
    // Normalize coordinates to [-1, 1] range centered at (0,0)
    vec2 uv = (gl_FragCoord.xy - resolution.xy * 0.5) / (resolution.y * 0.5);
    vec2 polar = cartesianToPolar(uv);
    
    // Calculate wavefront aberration by summing Zernike terms
    float density = 0.0;
    for (int i = 0; i < 15; i++) {
        density += zernikeCoeffs[i] * zernike(i, polar);
    }
    
    // Scale and convert to visible range
    density *= scale;
    float value = (density + 1.0) * 0.5; // Map [-1,1] to [0,1]
    value = clamp(value, 0.0, 1.0);
    
    // Output as grayscale density map
    FragColor = vec4(vec3(value), 1.0);
}