À propos de ce discours technique
Les modulateurs spatiaux de lumière (SLM) sont des composants optiques actifs capables de modifier l'amplitude, la phase ou la polarisation d'un faisceau lumineux. Pour cet exposé technique, je me concentrerai sur un sous-ensemble spécifique : ceux qui y parviennent à l'aide d'un réseau bidimensionnel pixellisé. Bien que cela ne couvre pas tous les types de SLM, il s'agit d'une catégorie suffisamment vaste et intéressante à explorer. Étant donné que ce blog est axé sur les intégrateurs de systèmes, je mettrai également en évidence les éléments clés à prendre en compte si vous décidez d'incorporer un SLM dans votre système.
Réflexion ou transmission
Pour commencer, nous avons deux grandes sous-catégories : les matériaux réfléchissants et les matériaux transmissifs. La plupart des SLM intéressants sur le plan industriel sont de type réfléchissant. La raison en est simple. Les appareils très performants nécessitent une plaquette CMOS pour distribuer les données sur l'appareil. La façon la plus simple d'y parvenir est de placer une couche métallique directement sur la tranche. Il est possible d'aménager une surface optiquement transmissible qui peut distribuer un signal électrique, mais cela implique des électrons libres qui ont tendance à interagir avec la lumière transmise. Le compromis que cela implique affecte généralement la vitesse de l'appareil ou la transmission optique.
Cela dit, on trouve encore de nombreux produits techniquement intéressants qui utilisent ce principe dans des applications grand public (comme les écrans LCD et certains projets basés sur le LCoS) et dans des environnements industriels.
SLM à amplitude réfléchissante
Il s'agit d'une classe importante de modulateurs spatiaux de lumière. Notamment, nous trouvons que le Le système DLP de Texas Instruments dans cette classe. Même si ce type de SLM modifie la phase de la lumière réfléchie, il n'est pas utilisé en tant que tel. Je m'explique. Le DLP est un dispositif à micro-miroirs purement réfléchissants où chaque micro-miroir ne peut avoir que deux états stables modifiant entre plus ou moins 12 degrés le long de sa diagonale, bien que l'angle puisse différer entre les différents types. Chaque point de la surface de ce dispositif modifie la phase de la lumière en introduisant une différence de trajet optique, mais comme ces phases ne sont pas indépendantes, nous ne pouvons observer que l'effet net d'un petit miroir incliné.
Il existe d'autres SLM fonctionnant selon le même principe optique, comme le Miroir basculant analogique IPMS SLM. Comme les dispositifs à miroir basculant sont globalement neutres en phase, ils dépendent du système d'imagerie pour exprimer l'effet recherché. Sans ce système, ils ressemblent simplement à une surface réfléchissante rugueuse. Avec un système de projection bien conçu, ils se transforment en systèmes de génération de motifs très performants qui ne peuvent être distingués des masques binaires de haute qualité.

Les dispositifs analogiques à miroir basculant sont simples à calibrer et à utiliser, mais nécessitent un laser Excimer pour atteindre leur véritable potentiel. Un miroir incliné dans le plan de l'image présente toutefois certaines propriétés qu'il convient de garder à l'esprit. L'inclinaison d'un miroir isolé ne peut jamais être cachée par le système optique, même si l'optique de projection est loin de résoudre le micro-miroir. Cela peut parfois être utilisé pour régler correctement la mise au point, peut-être même la manière la plus sensible de le faire sans interféromètre ou capteur de front d'onde, mais probablement seulement utile à des résolutions plus faibles.
La théorie de Fourier à la rescousse
Pour utiliser un tel dispositif à miroir basculant pour des applications haut de gamme, l'inclinaison du miroir doit être alternée (comme dans la figure ci-dessus). L'optique de projection annule alors la phase. D'une manière générale, c'est la théorie de Fourier qui permet le mieux de comprendre ces dispositifs.
Voici un exemple : Un dispositif comportant des miroirs plats présente un contraste infini, il suffit d'incliner les miroirs à l'angle correct. La plaque (ou le miroir) inclinée présente un schéma de réflexion donné par la fonction sincère et le zéro de cette fonction est l'angle correct pour un contraste infini. Que se passe-t-il lorsque nous utilisons un éclairage partiellement cohérent et que le SLM est éclairé avec une gamme d'angles d'incidence ? Cela signifie-t-il que le contraste est dégradé avec un éclairage partiellement cohérent ? Si nous nous en tenons à l'image sincère, nous pourrions être amenés à penser qu'il est impossible d'obtenir un angle d'inclinaison optimal puisque nous ne pouvons pas adapter simultanément un angle d'inclinaison à une gamme d'angles incidents. Si nous adoptons plutôt l'approche de Fourier, le réseau éclairé à une incidence nulle réfléchit toute la lumière le long de la normale. L'effet de l'inclinaison est représenté comme un ensemble de modes de diffraction qui ne seront pas transmis à travers la pupille. Pour toute onde plane hors axe, la lumière réfléchie n'est qu'une réplique décalée du motif sur l'axe. Si la première avait un contraste infini (lorsqu'elle est observée à travers l'optique de projection), la réplique l'est également. L'approche de Fourier donne la bonne réponse.
Défauts courants des appareils
Les dispositifs MEMS ne sont jamais parfaitement plats. Lorsque la surface polie sur laquelle ils sont fabriqués est résolue, il y a une libération mécanique des forces qui ajoute un déplacement vertical à courte portée. Cela introduit un chatoiement partiellement développé et d'autres effets. Il fixe la limite de la qualité d'image lors de l'utilisation de ces dispositifs. Tous les fabricants ne fournissent pas de spécifications concernant ces effets. Par exemple, je n'ai pas été en mesure de les trouver pour le Ti DLP. Toutefois, certaines limites de ce paramètre sont données par l'efficacité de la diffraction. Étant donné que le DLP doit superposer de nombreuses images pour générer une échelle de gris, le speckle partiellement développé ne devrait pas contribuer de manière significative à la dégradation de la qualité de l'image lors de l'utilisation de ces dispositifs.
Avec le temps, en particulier lors de l'utilisation de courtes longueurs d'onde, la surface supérieure peut subir un recuit et une compaction qui conduisent à une certaine courbure des miroirs. Pour le DLP, cela a un effet insignifiant sur la qualité de l'image en raison de l'inclinaison importante. Pour les dispositifs analogiques, il s'agit probablement de la propriété qui détermine la durée de vie utile du dispositif. Elle est visible sous la forme d'une dégradation du contraste, mais affecte d'autres propriétés d'imagerie importantes, telles que la sensibilité à la mise au point.
Amplitude linéaire SLMs
Les modulateurs linéaires ou unidimensionnels méritent probablement leur propre page, mais j'essaierai d'en présenter l'essentiel ici en parlant de deux dispositifs très différents. L'un est le Silicon Light Machines Grating Light Valve, ou GLV en abrégé. L'autre est le Fraunhofer IPMS 8k show de le présent document.
Ce qui rend les modulateurs 1D intéressants, c'est qu'ils peuvent utiliser une source laser continue ou quasi-continue. Dans le cas du GLV, il est même possible d'utiliser un laser Q-switché. Cette possibilité est très intéressante du point de vue du coût du système. Même si la fréquence de répétition du GLV est élevée pour un laser Q-switché, il existe encore de bonnes options. Le principal inconvénient du GLV est la façon dont il génère les niveaux de gris.
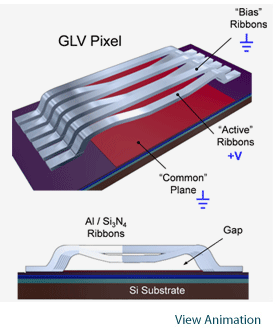
L'échelle de gris est générée en créant un réseau avec une profondeur variable, et donc une magnitude variable de lumière diffractée. Ce dispositif peut être utilisé à la fois à l'ordre 0 et à l'ordre 1, mais son contrat est nettement meilleur à l'ordre 1. Certaines variantes du dispositif combinent deux rubans pour former un pixel, tandis que d'autres utilisent 6 ou 3 paires de rubans. Cela n'a pas d'effet significatif sur les propriétés optiques de l'image.
Il est toutefois essentiel de garder à l'esprit que cette approche couple l'amplitude et la phase réfléchies, ce qui est critique pour la lithographie car cela entraîne une sensibilité à la mise au point si l'appareil est utilisé pour la mise à l'échelle des gris (ce qui est le plus souvent le cas). Une autre conséquence, peut-être pas si critique que cela, est que le minimum de réflexion ne peut pas être calibré si l'appareil est utilisé en ordre 0. On peut se demander comment calibrer un SLM qui ne réfléchit pas ou très peu la lumière. Disons simplement que le SLM à miroir basculant peut être facilement étalonné, tandis que le GLV y survit simplement parce qu'il n'est pas très sensible lorsqu'il est utilisé à proximité de l'amplitude réfléchie zéro. En référence au dispositif Fraunhofer, nous mentionnerons que le GLV doit être éclairé par une ligne étroite, d'une épaisseur de 5 à 10 microns. Cela signifie que nous devons tenir compte de la densité de puissance de crête lorsque nous utilisons ce dispositif.
Comment l'appareil Fraunhofer résout-il ce problème ? Ce dispositif a été conçu dès le départ pour traiter des sources continues de forte puissance. C'est pourquoi il est optiquement plat sur l'ensemble de ses 80×2 mm2 surface. Pour en tirer parti, le SLM doit être placé avant ou après la meilleure mise au point. Pour éviter une optique trop cylindrique, une image sans astigmatisme peut être rétablie en insérant une ou deux plaques parallèles inclinées.
Comme ce dispositif utilise des miroirs basculants, il est neutre du point de vue de la phase et ne présente pas d'effets de focalisation traversante lorsqu'il est utilisé comme SLM de mise à l'échelle des gris. Avant de passer à la section suivante, il convient de mentionner, au moins quelque part sur l'internet, que ce modulateur a été conçu pour une fréquence d'images de 2 MHz, et non de 1 MHz comme l'indique l'étude de cas. document lié (et la publication à ce sujet). La raison pour laquelle nous pouvons nous en sortir en pilotant un dispositif au-delà de sa fréquence de résonance nominale est que le modulateur a été conçu pour un facteur Q assez faible d'environ 1 et qu'un dispositif à échelle de gris ne peut de toute façon pas résoudre un seul pixel. En général, une bonne conception permet de résoudre 3 à 4 pixels, selon l'importance que l'on accorde à la qualité de l'image. Ces deux choix de conception ont permis à Micronic de piloter ce modulateur à 2 MHz. Avec un pixel de 1,25um (dans cette direction), la vitesse d'écriture était de 2,5 m/s. C'était quelque chose à voir.
SLM à phase réfléchissante
Les SLM à phase réfléchissante créent une différence de longueur de trajet principalement de deux manières. Soit en déplaçant la surface réfléchissante, soit en modifiant localement l'indice de réfraction afin de générer une différence de longueur de trajet. Les modulateurs spatiaux de lumière tels que le RealHolo, le PLM de Texas Instruments ou le PLV de Silicon Light Machines relèvent de la première catégorie. En termes de potentiel technique, le RealHolo se démarque clairement de la masse des MEMS.
Cristaux liquides sur silicium - LCoS
Une autre technologie SLM de phase populaire est celle des cristaux liquides sur silicium (LCoS). Ces micro-écrans reposent sur un ensemble assez complexe de technologies, notamment un fond de panier CMOS, une couche métallique de pixels, des couches d'alignement supérieure et inférieure pour les cristaux liquides, une couche d'oxyde d'indium et d'étain (ITO) pour générer le champ électrique à travers les cristaux liquides, et un verre de couverture pour maintenir l'ITO. Malgré cette complexité, les fabricants peuvent produire des panneaux LCoS en grandes quantités avec des rendements élevés et des défauts de pixels minimes.
Les panneaux LCoS offrent plusieurs avantages, dont la robustesse. Cependant, ils présentent également des inconvénients, tels que la dépendance à l'égard de la polarisation. En outre, l'épaisseur de la couche de cristaux liquides, déterminée par la longueur d'onde pour laquelle le SLM est conçu, limite la résolution effective du modulateur. Cette limitation découle de la nature des champs électriques, qui ont tendance à diverger à mesure qu'ils s'éloignent de leur source. Les panneaux LCoS sont essentiellement constitués de condensateurs transparents densément emballés, et lorsque la taille latérale de chaque condensateur est inférieure à la distance entre ses plaques, le champ électrique déborde sur les pixels voisins, créant une diaphonie. Dans l'industrie LCoS, ce phénomène est connu sous le nom d'effets de champ de frange. Il provoque à la fois des effets de polarisation indésirables et des effets de diaphonie. désinclinaisons. Avant d'aborder les MEMS SLM, nous devons mentionner un avantage majeur : vous pouvez les acheter aujourd'hui auprès d'entreprises telles que Hamamatsu ou Holoeye Photonics.
Matrices de miroirs à piston MEMS
Même si les dispositifs piston-MEMS ne sont pas aussi rares que les licornes, il est difficile d'en apercevoir un dans la nature. Cela dit, il n'en reste pas moins que les appareils à piston-MEMS ne sont pas rares, ils existent et si Texas Instruments finit par publier le PLM, ils pourraient en fait devenir assez courants. Les dispositifs à piston sont vraiment flexibles du point de vue optique. Il n'y a pas d'effets de polarisation à proprement parler. Il n'y a pas de dépendance par rapport à la longueur d'onde tant que l'on éclaire avec une seule longueur d'onde à la fois. Ils sont rapides et la phase est stable. Avec les LCoS, il faut fréquemment changer la polarité de la tension d'alimentation pour éviter la dégradation des cristaux liquides. Rien de tout cela ici. Une modulation de phase à 360 degrés et aucune interférence à signaler. C'est très bien. Je peux en avoir un paquet ? Il y a un problème, qui est également valable pour les panneaux LCoS : comment décider de la phase à appliquer à chaque pixel illuminé ?
Génération d'images avec des dispositifs à phase unique
En général, nous utilisons l'algorithme de Gerchberg-Saxton pour résoudre ce problème. Il est particulièrement utile dans les applications visuelles, où le cerveau rend le résultat plus acceptable. L'un des grands avantages des dispositifs à modulation de phase est qu'ils n'ont pas besoin d'optique. Illuminez avec un faisceau suffisamment large et vous obtenez un projecteur composé de deux parties, la source lumineuse et le SLM. La longueur d'onde et la taille du pixel limitent son étendue angulaire, mais si c'est suffisant, c'est fini. Sinon, nous pouvons utiliser un télescope galiléen pour obtenir le grossissement souhaité.
Pour la lithographie, où la qualité de l'image est primordiale, nous devons contrôler la phase réfléchie de la lumière. Si nous ne parvenons pas à le faire sur une longue distance, nos objets se déplacent à travers la mise au point. Si nous ne parvenons pas à le faire sur une courte distance, nous ajoutons du chatoiement à nos objets qui, en outre, augmentent avec les aberrations de notre optique de projection.
Il y a cependant un autre élément à prendre en compte. Comment déciderons-nous de la phase à définir pour chaque pixel ? Les méthodes de récupération de phase sont itératives et, à ma connaissance, renvoient une phase projetée aléatoire. Les méthodes directes que je connais utilisent des réseaux neuronaux, mais je n'ai pas vu quelle qualité d'image on peut en attendre. Je m'attends à ce que l'approche par réseau neuronal reproduise au mieux les résultats des méthodes d'extraction de phase utilisées pour l'entraîner. Par conséquent, je m'attends à ce que ces méthodes génèrent une phase aléatoire.
Quelques principes théoriques fondamentaux
En ce qui concerne la génération de motifs de haute qualité avec des modulateurs à phase seule, nous devons au moins identifier deux cas, l'un étant le cas de la cartographie linéaire, et l'autre, une cartographie non linéaire. Le cas de la cartographie linéaire correspond à la cartographie linéaire entre le modulateur et l'amplitude de l'image de l'imagerie cohérente, tandis que le cas non linéaire s'applique à l'imagerie partiellement cohérente.
Pour l'imagerie cohérente, nous savons que l'amplitude de l'image est une "fonction" linéaire de l'amplitude réfléchie,
Et quand P représente un dispositif discret, nous pouvons transformer l'intégrale en une somme en intégrant les "pixels",
Il y a des détails à ce sujet que nous pouvons ignorer pour le moment. Cependant, nous savons que, d'une manière ou d'une autre, nous pouvons inverser cette relation,
En pratique, l'inverse de H est généralement un pseudo-inverse, etc. Ce n'est pas la question. Cependant, même dans le cas simple où la réponse impulsionnelle H est réelle (c'est-à-dire que sa partie imaginaire est nulle) et que l'amplitude que nous cherchons à résoudre est également réelle, la solution (p) est alors réelle. Ce n'est pas vraiment une bonne solution pour un dispositif à piston.
Les pistons ont besoin d'une correspondance avec le cercle unitaire complexe
Il faut donc trouver un moyen de transformer un vecteur réel p (ayant NxM éléments, où NxM est la taille de notre SLM) en un vecteur,
où le vecteur h a la même taille que p. Nous voulons les hauteurs, hLe but est d'avoir la propriété que,
En d'autres termes, nous voulons annuler la partie imaginaire à l'aide du système optique. Je n'ai pas l'intention de transformer ce blog en un article de mathématiques, mais un système d'image bien conçu, destiné à l'échelonnement des gris, laissera une bonne marge de manœuvre pour la recherche de solutions h qui correspondent étroitement aux images générées par la cartographie Hp.
For linear mappings, or coherent systems in other words, there is quite a lot we can do to find a distribution of piston phases, without combining (say) 4 pixels to create an effective gray pixel, which would lead to 4 times writing capacity loss. We would need to dive into lots more math to describe the procuess fully, so maybe another time.
Quand le ciel n'est pas la limite SLM
Le modulateur à piston appliqué à la lithographie est le modulateur ultime pour ceux qui veulent pousser la résolution des sous-longueurs d'onde au-delà de ses limites pratiques, mais il a un coût. Voici ce qu'il en est. Un modulateur à piston peut projeter n'importe quelle phase et amplitude (en termes relatifs), mais pour la lithographie, nous ne voulons pas d'amplitude. Nous voulons que l'image ait une phase constante sur l'ensemble de l'image, car une variation de phase entraîne une variation des dimensions ou de l'emplacement de la caractéristique par rapport à la mise au point, ce que nous ne voulons absolument pas. Cela signifie que nous devons passer du temps à trouver une solution qui limite ce degré de liberté particulier de ce modulateur.
Pour avoir le beurre et l'argent du beurre, Micronic a inventé un miroir basculant qui comprenait un pas d'un quart de longueur d'onde sur la moitié du miroir. Le résultat était une amplitude d'image qui pouvait atteindre une plage (relative) de -1 à 1 et une variation de phase nulle. Toutes les bonnes choses pour lesquelles vous aviez besoin d'un miroir à piston sans le travail. L'inconvénient était une réduction de la réflectivité du dispositif, ce qui, pour une application comprenant un laser Excimer, n'était pas un problème. À proprement parler, il peut y avoir des topologies 2D que ce modulateur ne peut pas traiter en une seule image. Quoi qu'il en soit, ASML a décidé d'utiliser cette solution pour son géant de l'écriture directe.. Malheureusement, ASML n'a jamais commercialisé ce produit. À ma connaissance, il s'agit du plus grand SLM conçu et fabriqué à ce jour. 11 millions de miroirs de 8 microns à inclinaison analogique et un taux de répétition de l'image de 6 kHz. Vous pouvez trouver une belle image Image SEM ici.
En savoir plus
Si vous souhaitez en savoir plus, n'hésitez pas à me contacter par le biais de la page de contact ou simplement en envoyant un courriel à [email protected]. J'aime parler des SLM. Vous pouvez également laisser un commentaire ici.




Laisser un commentaire