Interferometer – or – Wavefront Sensor

Technology is developing, and so are wavefront sensors. Among notable improvements has been wavefront sampling density. Examples of such sensors are the HASO LIFT sensors offered by Imagine Optics and the QWLSI sensor by Phasics. The techniques to achieve this enhanced sampling density differ.

The LIFT technique, which also stands for Linearized Focal-plane Technique, is a new take on the method, which in the old days was used to keep focus in DVD and CD players. A cylindrical lens was added to provide additional (on-axis) astigmatism in the reflected beam path. When the disk was in focus, the quadrant detector would show the same signal in the two diametrically opposing cells. Out of focus, there was a difference, including sign, which could be used as feedback.

In the same spirit, the LIFT technique adds on-axis astigmatism, but samples the focal point with much higher resolution, and in this way, can resolve many more terms than a simple wavefront curvature.

Phasics QWLSI approach, on the other hand, employs interference to create a two-dimensional fringe pattern. Using Fourier fringe methods, two wavefront gradients are extracted and integrated to obtain the wavefront.

Interferometry, accuracy & resolution

Although it seems LIFT and QWLSI have nothing in common, they do. None of them can measure the deflection in absolute terms on the deformable mirror system sketched below. Does this matter? Well, it depends on what one wants to achieve. What it will do quite well is to measure the shape of the mirror given the signal, which in many instances is quite good enough. For the example in the sketch below, where we cannot see the entire mirror, we are out of luck.

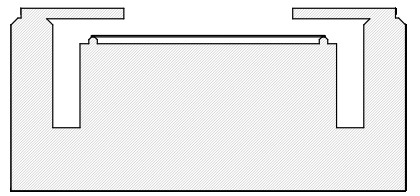
The piston term, so often ignored, is not a figment of anyone’s imagination. For a properly designed interferometer, it can be a reliable asset for all kinds of applications. This deformable mirror is perhaps esoteric, but calibration of a liquid crystal phase modulator can make good use of it. The optical case is quite similar. The clear aperture does not connect to a fixed phase, and fringe fields devalue the effectiveness of using the integrated value of a phase gradient.

Accuracy and open degrees of freedom

First, what do I mean with open degrees of freedom? With this, I mean degrees of freedom that directly contribute to the measurement error. They can be calibrated, and usually they are, but it is a linear sensitivity. An archetypical example of this is the displacement of the micro-lenses in a micro-lens array which, unless calibrated, render Shack-Hartmann sensors practically useless for accurate wavefront measurements. Are camera pixel sensitivities open? For the Shack-Hartmann sensor, the linear detector sensitivities appear open, since they individually reshape the recorded intensities, but under the assumption that the sensitivities remain linear and constant, they disappear in the already present calibration of spot centers.

Are interferometers necessarily accurate? No, obviously not. Many things contribute to the total error. However, compared to most wavefront sensing solutions, as optical system designers, we can have some level of control. Since at Senslogic we develop our own Shack-Hartmann sensor, we appreciate the value of calibrating these devices and the effort that goes into that. That said, when it comes to ultimate accuracy, nothing beats metrology whose accuracy can be traced to a single precision element.

The perfect example for that is the phase-shifting interferometer, or maybe I should have written, a phase-shifting interferometer to emphasize that phase-shifting is something that augments some specific interfe-rometer.

Phase-shifting

Let’s do a short review of the phase-shifting method, and what’s so special about it. Practically any interferometric setup can be augmented by phase-shifting, which means that one of the two paths the light can take adds an additional and well known sub-wavelength distance in order to turn fringe analysis into a simple equation for the relative phase between the paths.

Phase-shifting is by no means a new technology, and in the past literature you will find quite elaborate methods involving many phase steps in order to overcome the shortcomings of the prevailent technology available at the time. However, the 90° phase step, introduced from the very beginning, offers so much built-in error cancellation that, for at least two decades, there was no reason to use anything else to analyze a two-beam interference setups.

The resulting expression for the phase,

where the index denotes the number of 90° steps whe have done with our actuator. A and B are the real amplitudes of the two interfering beams, real because we have moved the phase difference between them into the phase. Even more importatnt is it to note that, when the intensities are recorded on a camera, each pixel gives us one of the above pair of expressions to solve, where we just divide,

The above expression is now free from both A and B. This is actually a bigger deal that may be immediately obvious because both A and B depend on the sensitivity of the camera pixels that happens to record them at the given position, and now they are gone. What we also didn’t mention that each of the intensities may have been recorded in a lab where there is a background light source. This contribution disappeared in the difference between intensities in both numerator and denominator.

The 90° phase-stepping is sometimes applied as a 4+1 measurement where the (seemingly) redundant phase shift of 360&\deg; is measured. Rudantant as it may seem, the 4+1 approach supresses second and even 3rd order detector non-linearities and actuator scale errors. The PSI module in WaveMe offers both the 4-image and (4+1) image methods, which if not for anything else, can be used to verify that the assumption we may have regardign our setup are correct.

With phase-shifting, we primarily need to make sure that the differences between the captured intensities only reflect the effect of our actuator, and since the images are recorded at different times, any time variation will appear as an error. There are methods that capture all the four phases simultaneously, but this requires a quite different camera and the error analysis will also look quite different. James C. Wyant is a much respected proponent of this approach.

Summary

With this tech-talk, I wanted to illuminate some things to consider when facing the choice of using a Shack-Hartmann sensor or an interferometer. If you choose the former, there are high-resolution products on the market. If the resolution is not what you are looking for, there isn’t much you can do except looking for another solution. The same goes if you need the piston term, or the average of the path length difference. Your choice is then the phase-shifting interferometer. If you’re not happy with the resolution, pick another camera. This changes nothing in the application. No new calibration. Just to take an example from my own past, where I happened to use whatever was at the table at the moment, which was a camera intended for video (not that it’s such a big difference), but the point is, with so much builtin compensation, you don’t have to care all that much beyond your own optical setup.