Die Entwicklung neuer optischer Systeme von Grund auf kann eine einschüchternde Aufgabe sein, vor allem, wenn es sich um ein System handelt, das wir erst einmal richtig hinbekommen müssen, bevor es gebaut werden kann, weil die entscheidenden Komponenten einfach noch nicht existieren. Es ist lediglich ein Hirngespinst, und es ist eigentlich Teil unserer Aufgabe, es zu definieren. Ähnliche Situationen entstehen, wenn wir verschiedene Entwürfe erforschen und lernen wollen, wie die Dinge tatsächlich funktionieren, bevor wir uns an die Aufgabe machen, sie zu bauen.
Stellen wir uns also Folgendes vor. Sie müssen die Anforderungen für ein System finden, das wir noch nie untersucht haben, und wenn es eine wissenschaftliche Arbeit gibt, die vielleicht mit dem, was wir brauchen, zusammenhängt, werden wir sie überhaupt finden? Es ist nicht ungewöhnlich, dass wir das Rad neu erfinden. Dirac hat die Clifford-Algebra neu erfunden, als er die Quantengleichungen für das Elektron ableitete, also passiert das natürlich auch den Besten von uns. Gehen wir also einfach davon aus, dass wir in jedem Fall die Verantwortung tragen.
Die beste Strategie an diesem Punkt wäre, ein Modell zu erstellen - eine Art Karte, aber nicht irgendeine Karte; sie muss detailliert genug sein, um durch alle wichtigen Drehungen und Wendungen (sprich: Freiheitsgrade) zu navigieren, aber nicht so kompliziert, dass wir den Wald vor lauter Bäumen nicht mehr sehen. Hier liegt unsere erste Herausforderung: Wenn diese Maschine nicht ein enger Verwandter von etwas ist, das wir bereits beherrschen, ist unsere Karte eher eine Vermutung als ein Evangelium. Wir tappen ein wenig im Dunkeln, welche Pfade (Freiheitsgrade) die relevanten sind und welche nur Details darstellen.
Ohne den richtigen Kompass (die richtigen Werkzeuge), um sich in der Komplexität zurechtzufinden, laufen wir Gefahr, unsere Karte zu stark zu vereinfachen und uns mehr von unserer Vorstellungskraft als vom tatsächlichen Terrain leiten zu lassen.
Reduzierung der Komplexität
Eine Möglichkeit, damit umzugehen, die sich meiner Meinung nach bewährt hat, ist die Verwendung einer bekannten mathematischen Erweiterung um den Idealzustand des untersuchten Systems, im Wesentlichen eine Maclaurin-Erweiterung. Da wir ein Werkzeug suchen, das unsere Analyse von unseren eigenen mentalen Beschränkungen befreit, muss es eines sein, das uns erlaubt, unser System mit einer großen Anzahl unabhängiger Variablen zu untersuchen.
Es gibt verschiedene Möglichkeiten, dies anzugehen, aber eine, die meiner Erfahrung nach sehr gut funktioniert, ist das so genannte Latin Hypercube Sampling (LHS), das manchmal auch als raumfüllendes Design bezeichnet wird.
Die Erstellung einer LHS nimmt einige Zeit in Anspruch, aber in den meisten Fällen dauert sie weniger als ein paar Minuten, selbst wenn die Anzahl der unabhängigen Variablen groß ist. Die Zeit für die Erstellung einer LHS wächst linear mit der Anzahl der Variablen und mit der dritten Potenz der Anzahl der Stichproben. Potenz mit der Anzahl der Stichproben. Glücklicherweise ist dies nur polynomiale Komplexität, oder "einfach", wenn Sie Leute aus dem Bereich der Computerkomplexität fragen.
Ein Beispiel dafür, dass eine große Anzahl von DOFs interessant sein kann, ist, wenn man eine Spezifikation für ein optisches System ableiten möchte und die DOFs die Koeffizienten des Zernike-Polynoms sind.
Die LHS liefert uns eine Reihe von gleichmäßig verteilten Stichproben in einem mehrdimensionalen Raum, aber es liegt immer noch an uns, die richtige Frage zu stellen, und in diesem Fall gibt es praktisch keine falschen Fragen.
So kann man z. B. mit diesem Satz von Stichproben eine Reihe von Simulationen erstellen, die die Varianz der Eigenschaft untersuchen, oder man kann simulieren, wie eine deterministische Eigenschaft von unseren DOF abhängt. Beides kann sehr wertvoll sein, aber bevor wir tiefer in die Materie eintauchen, lassen Sie uns darüber sprechen, wie wir einige Ergebnisse zur Analyse erhalten.
Exapansion zweiter Ordnung
So simpel dies auch klingen mag, es ist ein sehr wertvoller Ansatz, der zu Einsichten führt, die nicht selten zu Aha-Erlebnissen werden.
Von der LHS haben wir eine Reihe von Punkten, und wenn wir diese Stichprobenpunkte für unser mehrdimensionales Problem verwenden, führen wir eine gleiche Anzahl von Simulationen durch, um ein numerisches Ergebnis für jeden Punkt zu erhalten. Das alles ist jedoch nicht sehr aufschlussreich. Wir müssen diese Komplexität reduzieren. Wir müssen all diese Simulationen, die leicht mehrere Tausend sein können, in etwas zusammenfassen, das wir erfassen können, etwas, das sozusagen die Spreu vom Weizen trennt.
Der Weg dazu ist der Versuch, unsere Ergebnisse durch eine Erweiterung zweiter Ordnung auszudrücken,
Dies ähnelt sehr der Art und Weise, wie wir eine MacLaurin-Erweiterung ausdrücken würden, aber der Punkt ist, dass der Gradient und die Hessian immer noch unbekannt sind und wir sie finden müssen. Können wir das tun?
Ja, das können wir. Wir haben eine Fülle von Informationen und finden den Koeffizienten von v und H ist ein lineares Problem. Für eine 2 DOF haben wir 1 Unbekannte "c", zwei Unbekannte im linearen Term "v" und 2 + 1 in "H", denn H ist symmetrisch. Für 3 DOF haben wir 1 + 3 + 3 + 2 + 1 und so weiter. Das ist einfach lineare Algebra. Unsere Tausenden von Simulationen und die Pseudo-Inverse von More Penrose werden uns diese Unbekannten schneller liefern, als wir "numerische Lösung" sagen können.
Zu den guten Sachen
Und jetzt beginnt der interessante Teil. Unter der Annahme, dass unsere Expansionen 2. Ordnung gut sind, haben wir oft Tausende von Simulationen zu einem Modell reduziert, das wir jetzt noch weiter auseinandernehmen können.
Das erste, was man in der Regel tut, nachdem man die Erweiterung erhalten hat, ist zu prüfen, wie gut diese Erweiterung die Tausenden von simulierten Ergebnissen reproduziert. Oftmals ist die Korrelation zwischen dem Modell und den Simulationen größer als 99%. Ich würde 95% als kaum brauchbar ansehen, aber das übliche Ergebnis liegt bei 99% oder besser. Es hängt natürlich davon ab, wie die zugrunde liegende Eigenschaft aussieht, ob unser numerisches Modell für eine statistische Eigenschaft steht oder nicht.
Bevor wir mit diesem Modell gespielt haben, wissen wir das nicht, aber ich habe noch keinen Fall gefunden, der nicht in irgendeiner Weise transformiert werden könnte, so dass diese Erweiterung im Wesentlichen die gesamte Varianz aus unseren Simulationen erfassen kann.
Analyse der Expansion
Jetzt kommen wir zu dem Teil, wo wir die Früchte unserer harten Arbeit ernten können. Es gibt in der Regel drei Arten von Ergebnissen: Entweder wird die Ausdehnung durch den linearen Term oder den quadratischen Term dominiert oder sie ist gemischt, was eigentlich recht interessant ist, weil es uns sagt, dass unsere Ausdehnung nicht um ein Minimum herum ist.
Wenn der lineare Term dominiert, dann war's das wohl. Es gibt keine Wechselwirkungen zwischen den DOFs, über die man reden müsste. Der Fall ist abgeschlossen. Unser System war einfach, und wenn wir es vorher nicht verstanden haben, so wissen wir es jetzt.
Interessanter wird es, wenn der Term zweiter Ordnung die Expansion dominiert, denn jetzt gibt es mehr zu lernen. Hier sollte man auf jeden Fall mehr lineare Algebra in Anspruch nehmen und Folgendes umschreiben H als,
mit Hilfe der Singulärwertzerlegung (Singular Value Decomposition, kurz: SVD).
Wenn Sie so weit gekommen sind und sich dafür entscheiden, diese Gelegenheit nicht zu nutzen, wäre das gleichbedeutend damit, dass Neo die blaue Pille schluckt und sich dafür entscheidet, zu schlafen und zu glauben, was er glauben will. Nehmen Sie niemals die blaue Pille.
Wenn Ihr System in Form einer Matrix zweiter Ordnung ausgedrückt werden muss, müssen Sie im Wunderland bleiben und sich von der SVD zeigen lassen, wie tief das Kaninchenloch ist.
Dies ist nicht nur ein theoretisches Zahlenspiel. Sie müssen das wissen, wenn Sie Ihre Optik entwerfen, denn es sagt Ihnen nicht nur, dass bestimmte Kombinationen von Abbildungsfehlern zusammen optimiert werden müssen, sondern die Diagonalelemente von Σ sagen Ihnen auch, wie wichtig jede dieser Kombinationen wirklich ist, was ein unschätzbarer Hinweis darauf ist, was die Merit-Funktion am meisten unterdrücken sollte.
Wie sieht es nun mit dem gemischten Fall aus, bei dem sowohl der lineare als auch der quadratische Teil wesentlich zum Modell beitragen? Dieser Fall ist wirklich interessant, weil er uns zeigt, dass das System entgegen unserer ursprünglichen Annahme nicht um den idealen Zustand herum erweitert wurde.
In diesem Fall ist ein wenig Vorsicht geboten, da die Lösung modellabhängig ist, und selbst dann kann sie auf ein neues Minimum i außerhalb des Volumens hinweisen, das von der anfänglichen Gruppe von Probenahmestellen untersucht wurde. Das kann immer noch in Ordnung sein, aber es kann nicht als selbstverständlich angesehen werden.
Es ist Zeit für ein Beispiel
Nehmen wir an, wir würden diese Theorie auf etwas wie die Faserkopplung anwenden. In der Annahme, dass wir nicht wissen, wie es funktioniert, verwenden wir die Zernike-Polynome als Freiheitsgrade und berechnen als Testfunktion die Einfügedämpfung in Abhängigkeit von unseren Freiheitsgraden.
Zunächst müssen wir festlegen, wie viele DOF wir untersuchen wollen. Sagen wir, dass wir bei Z16 aufhören. Wir wissen, dass Z1 normalerweise keine Rolle spielt, aber die folgenden schon, also 15 DOF.
Als Nächstes erzeugen wir mit der LHS 1024 Stichprobenpunkte über 15 DOF. Die LHS generiert normalerweise Stichprobenpunkte über einen Hyperwürfel, so dass wir diese Werte auf einen vernünftigen Wert skalieren müssen. Wenn wir nichts über den Gegenstand wissen, sollten wir wahrscheinlich klein anfangen, wirklich klein. Dann können wir den Prozess so lange wiederholen, bis wir feststellen, dass das von uns berechnete Modell nicht mehr sehr gut zu den Daten passt, oder bis wir einen Wertebereich erreichen, den wir für unser System als relevant erachten.
Nun machen wir einen kleinen Zeitsprung und 1024 Simulationen der Einfügedämpfung später haben wir unsere Funktion f(x,....) und etwas zu modellieren. (Bei dieser Simulation wurde eine Apodisierung von 2 und eine gaußförmige Grundmode angenommen. In diesem Blog geht es nicht so sehr um Singlemode-Fasern, verzeihen Sie also die vereinfachten Annahmen über Singlemode-Fasern).
Sobald wir die Koeffizienten von c, v, und Hkönnen wir uns ansehen, wie das Modell unsere Simulationen erfasst hat,
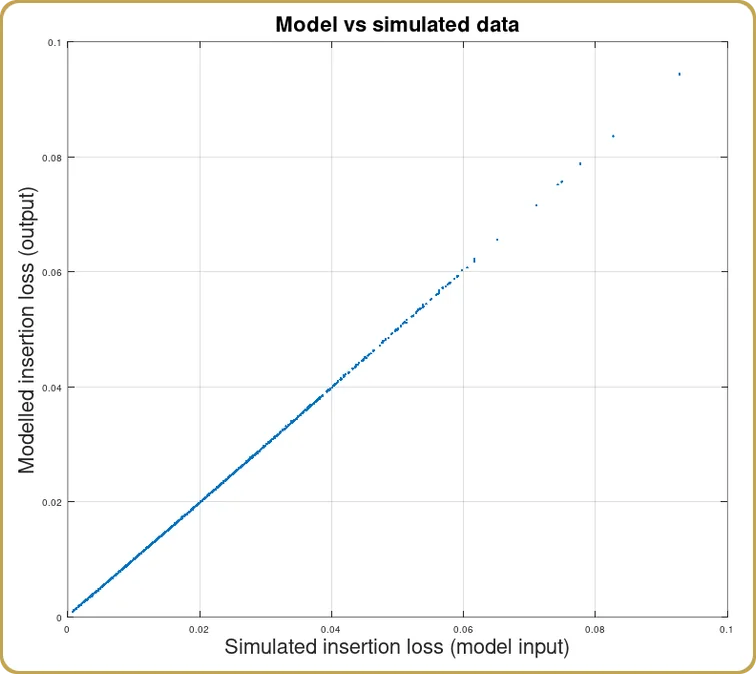
Wie erwartet, ergab sich eine gute Korrelation zwischen den Simulationen und der Modellexpansion. Da die physikalische Optik nur durch das Überlappungsintegral beschrieben wird, war das auch zu erwarten. Schließlich soll dies ein Beispiel sein, von dem man lernen kann.
Nun können wir uns auch ansehen, wie viel von dieser Korrelation auf den linearen Term zurückzuführen ist,
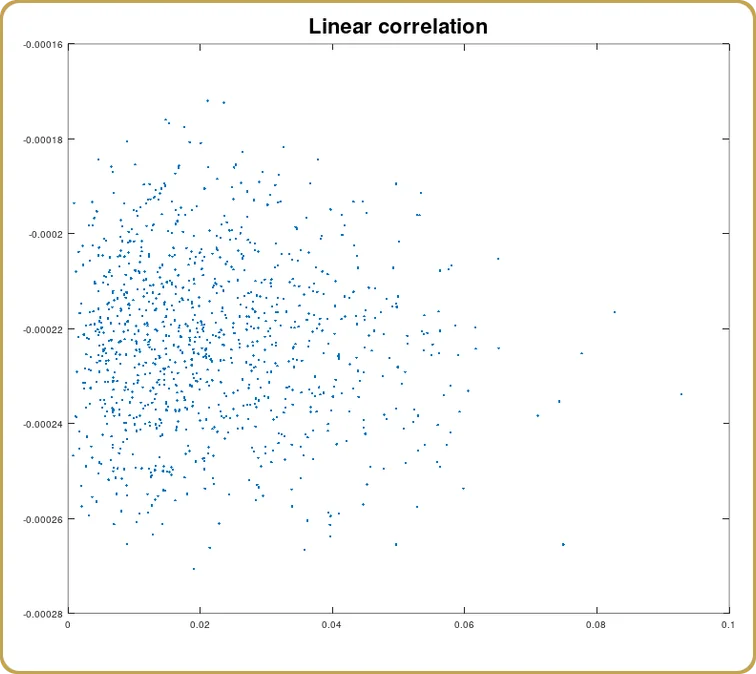
Und wieder ist die Korrelation erwartungsgemäß eine (statistische) Null. Wir haben etwas modelliert, das bei Null-Abweichungen ein Minimum hat. Es wird erwartet, dass der lineare Teil verschwindet. Schauen wir uns nun den quadratischen Term an.
Ich hoffe, dass es mittlerweile ziemlich offensichtlich ist, dass wir die Singular Value Decomposition verwenden werden, erinnern Sie sich an die rote Pille, richtig? Also, wir werfen unsere H in die SVD ein, und das erste, was zu prüfen ist, sind die Singulärwerte,
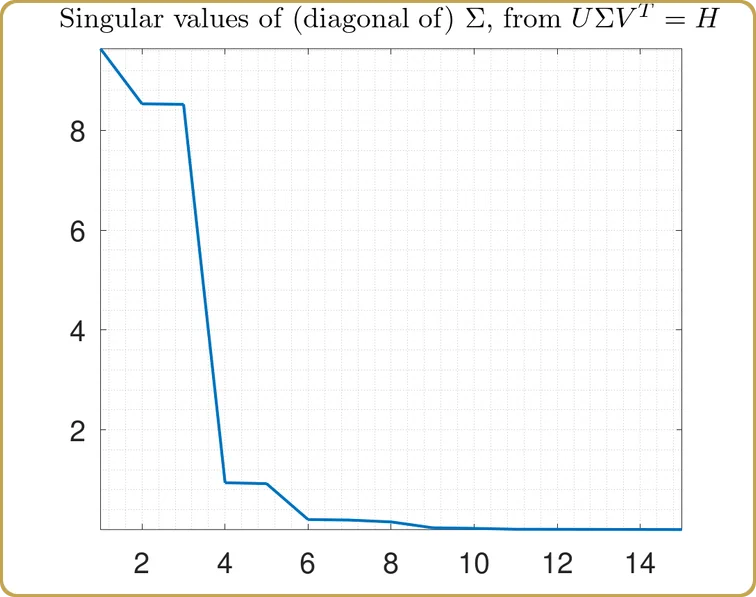
Die tatsächlichen Werte auf der Y-Achse sind nicht so interessant, denn sie hängen vom Volumen unseres Test-Hyperwürfels ab, den wir für die Stichprobe unseres Problems verwendet haben. Was interessanter ist, ist die Struktur. Unser Problem hat sich auf fast 3 unabhängige Variablen reduziert, plus 2 viel weniger wichtige. Schauen wir uns das mal an,
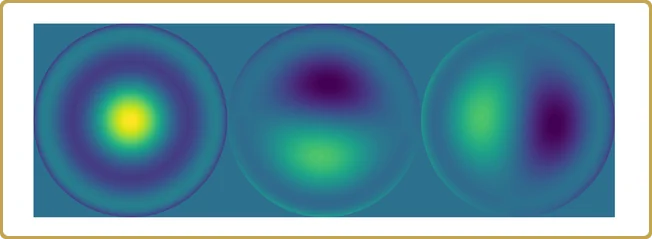
Zeit für ein Resümee.
Wir begannen mit 1024 simulierten Werten über 15 Dimensionen von etwas, von dem wir (vorgaben) nichts zu wissen, und endeten mit 3 wichtigen Beiträgen zu einer Eigenschaft, die wir verstehen wollten.
Dies ist kein ungewöhnliches Ergebnis bei dieser Art von Analyse. Vielleicht ist die Korrelation nicht ganz so gut wie in diesem konstruierten Beispiel, aber mit einer gewissen Transformation der Daten kann das Modell zweiter Ordnung im Wesentlichen die gesamte Varianz der Simulation erfassen.
Der vielleicht wertvollste Aspekt dieser Art von Analyse ist, dass wir eine viel größere Anzahl von Freiheitsgraden annehmen können und uns nicht durch unsere Fähigkeit einschränken, die Komplexität zu entwirren, oder um eine Verbindung zur Landkartenmetapher herzustellen: Es gibt keine Bäume. Alles, was wir sehen, sind Wälder und Hügel. Aus diesem Blickwinkel ist das große Ganze alles, was es gibt, und alles, was wir dafür bezahlt haben, war Computerzeit.
Systems engineers toolbox
There is a practical tool in here, for systems engineers who just need a way capture one of many moving parts in their (usually quite large) Excel sheet of system trade-offs.
It’s not always that one will find a textbook analysis like the one presented here. I’m wrinting this because I just run into one where there is no linear correlation, and no second order correlation, but the full expansion still captures 96%-97% of the data. This is not unusual when one mixes variables that are not physically connected. They usually don’t model well together.
However, the expansion still captured information which can be used when, we, as systems engineers need to trade between parameter that we capture in our (say) optical simulations against the effects these parameters may have on other system properties. Many such examples.
Going further
Why did we stop at a 2nd order expansion? Well, there are “reasons”. The next order is described by a symmetric rank-3 tensor. We can still extract the components of this tensor because the least-squares problem coupling these components to our data is still linear.
There are some things we loose though. There is no SVD for tensors, for example. However, there is “recent” mathematical work done here (if you call 2005 recent, but I started doing this before 2005, so), that may offer further insights into properties of complex systems, such as eigenvalues and eigenvectors for tensors.
If you find that too esoteric, and I completely understand if you do, a 3rd order expansion is guaranteed to capture more variance in your data than a second order. If you just need that magic function in your Excel sheet, at least you can have that.





Kommentar verfassen