Ist dies die richtige Basis für Ihr System?

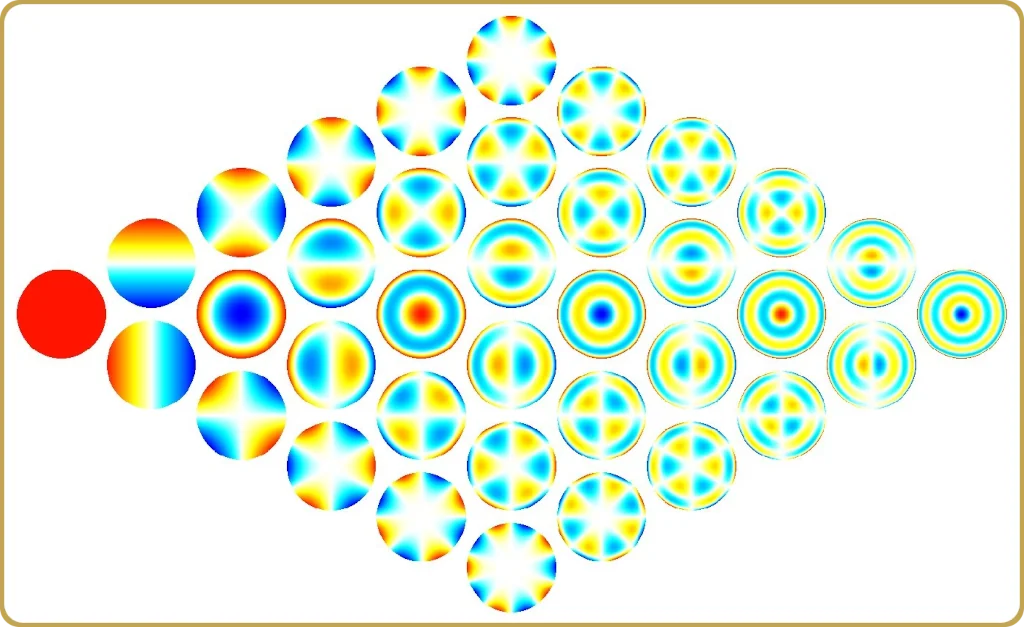
Die Zernike-Polynome kennen wir alle, und sie sind die Sprache, die wir oft verwenden, wenn wir optische Systeme beschreiben. Aber sind sie immer die richtige Sprache?

Gibt es eine falsche Sprache? Letztendlich würden wir versuchen, ein Design auf Null zu setzen, damit es keine Rolle spielt. Aber hey, null, das wäre so, als würde man nichts sagen.

Was ist, wenn wir nicht auf Null kommen können, oder wenn wir bei der Tolerierung entweder diesen oder jenen Begriff vorschieben können, aber nicht beide. Wie entscheiden wir uns? Wenn wir ein Teleskop bauen, ist der Fall klar. Wir wollen die Varianz des Wellenfronts minimieren und damit das Strehl-Verhältnis maximieren. Sehr deutlich abgeleitet in Born & Wolf.

Was aber, wenn die Eigenschaft, an der wir interessiert sind, nicht von der Varianz abgeleitet ist? Wie können wir das wissen?

Eine mögliche Analyse besteht darin, die MacLaurin-Erweiterung der interessierenden Eigenschaft bis zur zweiten Ordnung zu finden, indem man das Zernike-Polynom (z. B.) als Sonden oder einfach als freie Parameter verwendet. Man kann dazu einen Monte-Carlo-Ansatz oder einen Latin-Hypercube-Sampling-Ansatz verwenden, und welcher davon der beste ist, ist eine Diskussion, die an anderer Stelle zu führen ist. Sobald wir dies jedoch getan haben, können wir die c, v und A finden, die am besten zu den Daten passen, und diese Anpassung kann wirklich sehr gut sein.

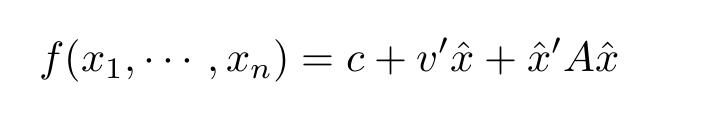
Wenn sich herausstellt, dass A in dieser Erweiterung nicht diagonal ist, dann sind die Zernike-Polynome nicht die richtige Sprache, denn es folgt nicht, dass die Minimierung eines der Koeffizienten immer die gewünschte Eigenschaft verbessert. In diesem Fall erhalten wir durch die Diagonalisierung von A eine neue orthogonale Basis.

Bevor wir uns jedoch die Frage stellen, welche der Terme zu minimieren sind, aber in der neuen Basis, was ist mit dem linearen Term v. Die Antwort darauf ist, dass es darauf ankommt. Es besteht natürlich die Möglichkeit, die Lösung von f = 0 zu betrachten, und wenn diese Lösung innerhalb des Gültigkeitsbereichs der Expansion liegt, haben wir wahrscheinlich eine nicht-triviale Lösung gefunden, bei der Abweichungen ungleich Null einen Nullfehler erzeugen. Das kommt vor, aber oft ist entweder v im Wesentlichen Null oder die Lösung für f = 0 liegt nicht im Gültigkeitsbereich der Expansion.

Wenn der lineare Term v gleich Null ist, stellt sich die gleiche Frage wie am Anfang: Sollen wir diesen oder jenen Term in der neuen Basis verbessern? Die Antwort lautet: Das spielt keine Rolle, denn solange wir die inkohärente (Quadratur-)Summe der Terme reduzieren, verbessert sich unsere interessante Eigenschaft.

Das ist zwar etwas esoterisch, aber wenn wir die Modelle für unser optisches System und die interessierende Eigenschaft haben, kann die Untersuchung von 15-20 freien Parametern mit ein paar tausend Simulationen durchaus machbar sein und wertvolle Erkenntnisse über die Grundlagen des optischen Systems liefern. Oft kann dies in weniger als einem Tag erledigt werden, wenn wir die Modelle bereits haben.