Über diesen Tech-Talk
Räumliche Lichtmodulatoren (SLMs) sind aktive optische Komponenten, die die Amplitude, Phase oder Polarisation eines Lichtstrahls verändern können. In diesem Tech-Talk konzentriere ich mich auf eine bestimmte Untergruppe: diejenigen, die dies mit einem zweidimensionalen Pixel-Array erreichen. Dies deckt zwar nicht alle Arten von SLMs ab, ist aber eine ausreichend große und interessante Kategorie, die es zu erkunden gilt. Da sich dieser Blog auf Systemintegratoren konzentriert, werde ich auch die wichtigsten Überlegungen hervorheben, wenn Sie sich entscheiden, ein SLM in Ihr System einzubauen.
Reflektierend oder transmissiv
Zunächst einmal gibt es zwei große Unterklassen: reflektierende und durchlässige. Die meisten industriell interessanten SLMs sind vom reflektierenden Typ. Der Grund dafür ist einfach. Leistungsstarke Geräte erfordern einen CMOS-Wafer, um die Daten über das Gerät zu verteilen. Der einfachste Weg, dies zu erreichen, besteht darin, eine metallische Schicht direkt auf einen Wafer aufzubringen. Es ist möglich, eine optisch durchlässige Oberfläche anzuordnen, die ein elektrisches Signal verteilen kann, aber das setzt freie Elektronen voraus, und diese neigen dazu, mit dem übertragenen Licht zu interagieren. Der dadurch entstehende Kompromiss wirkt sich in der Regel auf die Geschwindigkeit der Geräte oder die optische Übertragung aus.
Dennoch gibt es viele technisch interessante Produkte, die dieses Prinzip sowohl in Verbraucheranwendungen (wie LCD-Displays und einige LCoS-basierte Projekte) als auch in der Industrie nutzen.
Reflektierende Amplituden-SLMs
Dies ist eine wichtige Klasse von räumlichen Lichtmodulatoren. Bemerkenswert ist, dass wir die Der DLP von Texas Instruments in dieser Klasse. Auch wenn diese Art von SLMs die Phase des reflektierten Lichts verändern, werden sie nicht als solche verwendet. Lassen Sie mich das erklären. Der DLP ist eine rein reflektierende Mikrospiegelvorrichtung, bei der jeder Mikrospiegel nur zwei stabile Zustände haben kann, die sich zwischen plus oder minus 12 Grad entlang seiner Diagonale ändern, obwohl der Winkel zwischen verschiedenen Typen unterschiedlich sein kann. Jeder Punkt auf der Oberfläche dieses Geräts verändert die Phase des Lichts, indem er eine optische Wegdifferenz einführt, aber da diese Phasen nicht unabhängig sind, können wir nur den Nettoeffekt eines kleinen, geneigten Spiegels beobachten.
Es gibt andere SLMs, die nach dem gleichen optischen Prinzip arbeiten, wie z. B. das IPMS analoger Kippspiegel SLM. Da die Kippspiegelgeräte insgesamt phasenneutral sind, sind sie auf das Abbildungssystem angewiesen, um die beabsichtigte Wirkung zu erzielen. Ohne dieses sehen sie nur wie eine raue reflektierende Oberfläche aus. Mit einem richtig konzipierten Projektionssystem verwandeln sie sich in hochleistungsfähige Systeme zur Erzeugung von Mustern, die von hochwertigen binären Masken nicht zu unterscheiden sind.

Die analogen Kippspiegelgeräte sind einfach zu kalibrieren und zu verwenden, benötigen aber einen Excimer-Laser, um ihr wahres Potenzial auszuschöpfen. Es gibt jedoch einige Eigenschaften, die ein gekippter Spiegel in der Bildebene mit sich bringt, die man im Auge behalten sollte. Die Kippung eines isolierten Spiegels kann durch das optische System nicht verdeckt werden, selbst wenn die Projektionsoptik den Mikrospiegel nicht einmal annähernd auflöst. Dies kann manchmal genutzt werden, um den Fokus richtig einzustellen, möglicherweise sogar die empfindlichste Art, dies ohne Interferometer oder Wellenfrontsensor zu tun, aber wahrscheinlich nur bei niedrigeren Auflösungen nützlich.
Die Fourier-Theorie als Retter in der Not
Um ein solches Kippspiegelgerät für High-End-Anwendungen zu verwenden, muss die Spiegelneigung alternierend sein (wie in der Abbildung oben). Die Projektionsoptik hebt dann die Phase auf. Im Allgemeinen lassen sich diese Geräte am besten mit Hilfe der Fourier-Theorie verstehen.
Hier ist ein Beispiel: Ein Gerät mit flachen Spiegeln hat einen unendlichen Kontrast, man muss die Spiegel nur in den richtigen Winkel kippen. Die gekippte Platte (oder der Spiegel) hat ein Reflexionsmuster, das durch die sinc-Funktion gegeben ist, und der Nullpunkt dieser sinc-Funktion ist der richtige Winkel für unendlichen Kontrast. Was passiert, wenn wir eine teilkohärente Beleuchtung verwenden und der SLM mit einer Reihe von Einfallswinkeln beleuchtet wird? Bedeutet das, dass der Kontrast bei teilkohärenter Beleuchtung verschlechtert wird? Bleibt man bei dem Sinusbild, könnte man meinen, dass es unmöglich ist, einen optimalen Kippwinkel zu finden, da man den einen Kippwinkel nicht gleichzeitig an einen Bereich von Einfallswinkeln anpassen kann. Wenn wir stattdessen den Fourier-Ansatz wählen, reflektiert das bei Nulleinfall beleuchtete Array das gesamte Licht entlang der Normalen. Die Wirkung der Neigung wird als eine Reihe von Beugungsmoden dargestellt, die nicht durch die Pupille übertragen werden. Für jede außermittige ebene Welle ist das reflektierte Licht nur ein verschobenes Abbild des achsnahen Musters. Wenn das erste Muster unendlich kontrastreich war (wenn es durch die Projektionsoptik betrachtet wird), dann ist es auch die Nachbildung. Der Fourier-Ansatz liefert die richtige Antwort.
Häufige Gerätefehler
MEMS-Bauteile sind nie vollkommen flach. Wenn die polierte Oberfläche, auf der sie hergestellt werden, aufgelöst wird, kommt es zu einer mechanischen Freisetzung von Kräften, die eine kurzzeitige vertikale Verschiebung bewirkt. Dies führt zu einer teilweisen Entwicklung von Flecken und anderen Effekten. Dies setzt der Bildqualität bei der Verwendung dieser Geräte Grenzen. Nicht alle Hersteller machen Angaben zu diesen Effekten. Für den Ti DLP zum Beispiel konnte ich keine Angaben finden. Einige Grenzen für diesen Parameter werden jedoch durch die Beugungseffizienz gesetzt. Da der DLP viele Bilder überlagern muss, um eine Graustufe zu erzeugen, sollten teilweise entwickelte Speckle bei der Verwendung dieser Geräte nicht wesentlich zur Verschlechterung der Bildqualität beitragen.
Mit der Zeit, insbesondere bei der Verwendung kurzer Wellenlängen, kann die obere Oberfläche ausglühen und sich verdichten, was zu einer gewissen Krümmung der Spiegel führt. Bei DLP-Geräten hat dies aufgrund der großen Neigung nur unbedeutende Auswirkungen auf die Bildqualität. Bei analogen Geräten ist dies wahrscheinlich die Eigenschaft, die die nutzbare Lebensdauer des Geräts bestimmt. Sie ist als Kontrastverschlechterung sichtbar, beeinträchtigt aber auch andere wichtige Abbildungseigenschaften wie die Schärfeempfindlichkeit.
Lineare Amplitude SLMs
Die linearen oder eindimensionalen Modulatoren verdienen wahrscheinlich eine eigene Seite, aber ich werde versuchen, hier einige der wesentlichen Dinge zu erläutern, indem ich über zwei sehr unterschiedliche Geräte spreche. Das eine ist das Silicon Light Machines Grating Light Valve, kurz GLV. Das andere ist die Fraunhofer IPMS 8k Show in dieses Dokument.
Das Interessante an den 1D-Modulatoren ist, dass sie eine kontinuierliche oder quasi-kontinuierliche Laserquelle verwenden können. Im Falle des GLV kann sogar ein gütegeschalteter Laser verwendet werden. Dies ist aus Sicht der Systemkosten sehr attraktiv. Auch wenn die Wiederholfrequenz des GLV für einen gütegeschalteten Laser eher hoch ist, gibt es dennoch gute Optionen. Der größte Nachteil des GLV ist die Art und Weise, wie er Graustufen erzeugt.
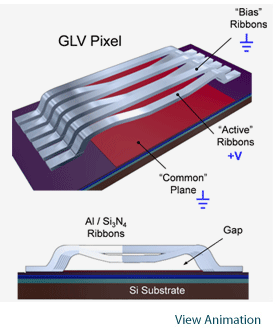
Die Grauskala wird durch die Erzeugung eines Gitters mit variabler Tiefe und damit variabler Stärke des gebeugten Lichts erzeugt. Dieses Gerät kann sowohl in 0. als auch in 1. Ordnung verwendet werden, hat aber einen deutlich besseren Vertrag in 1. Einige Varianten des Geräts kombinieren zwei Bänder zu einem Pixel, während andere 6 oder 3 Bandpaare verwenden. Dies hat keine wesentlichen Auswirkungen auf die optischen Bildeigenschaften.
Es ist jedoch zu beachten, dass bei diesem Ansatz die reflektierte Amplitude und die Phase gekoppelt werden, was für die Lithografie kritisch ist, da es zu einer Empfindlichkeit des Fokus führt, wenn das Gerät für die Grauskalierung verwendet wird (was meistens der Fall ist). Eine weitere, vielleicht nicht ganz so kritische Folge ist, dass das Reflexionsminimum nicht kalibriert werden kann, wenn das Gerät in 0ter Ordnung verwendet wird. Man könnte sich fragen: Wie kalibriert man ein SLM, das kein oder nur sehr wenig Licht reflektiert? Sagen wir einfach, dass der Kippspiegel-SLM leicht kalibriert werden kann, während das GLV dies einfach dadurch übersteht, dass es nicht sehr empfindlich ist, wenn es nahe der Null-Reflexionsamplitude betrieben wird. Als Anspielung auf das Fraunhofer-Gerät sei erwähnt, dass das GLV mit einer schmalen, 5-10 Mikrometer dicken Linie beleuchtet werden muss. Dies bedeutet, dass wir die Spitzenleistungsdichte berücksichtigen müssen, wenn wir dieses Gerät verwenden.
Wie also löst das Fraunhofer-Gerät dieses Problem? Dieses Gerät wurde von Anfang an für den Umgang mit kontinuierlichen Hochleistungsquellen entwickelt. Daher ist das Gerät über seine gesamte Fläche von 80×2 mm optisch flach.2 Oberfläche. Um dies auszunutzen, muss das SLM vor oder nach dem besten Fokus platziert werden. Um eine zu zylindrische Optik zu vermeiden, kann ein astigmatismusfreies Bild durch Einsetzen einer oder zweier geneigter paralleler Platten wiederhergestellt werden.
Da dieses Gerät Kippspiegel verwendet, ist es phasenneutral und zeigt keine Durchschärfeeffekte, wenn es als Grauskalierungs-SLM verwendet wird. Bevor wir zum nächsten Abschnitt übergehen, sollte zumindest irgendwo im Internet erwähnt werden, dass dieser Modulator für eine Bildwiederholrate von 2MHz und nicht von 1MHz wie die verlinktes Dokument (und die Veröffentlichung darüber) behauptet. Der Grund, warum wir ein Gerät oberhalb seiner Nennresonanzfrequenz betreiben können, ist, dass der Modulator für einen recht niedrigen Q-Faktor von etwa 1 ausgelegt ist und ein Graustufengerät ohnehin keine einzelnen Pixel auflösen kann. Normalerweise löst ein gutes Design 3 bis 4 Pixel auf, je nachdem, wie viel Wert wir auf die Bildqualität legen. Dank dieser beiden Designentscheidungen konnte Micronic diesen Modulator mit 2 MHz betreiben. Mit einem 1,25-µm-Pixel (in dieser Richtung) ergab sich eine Schreibgeschwindigkeit von 2,5 m/s. Das war wirklich beeindruckend.
SLMs mit reflektierender Phase
Reflektierende Phasen-SLMs erzeugen eine Weglängendifferenz meist auf zwei Arten. Entweder durch Verschiebung der reflektierenden Oberfläche oder durch lokale Änderung des Brechungsindexes, um eine Weglängendifferenz zu erzeugen. Im ersten Fall handelt es sich um räumliche Lichtmodulatoren wie den RealHolo, den Texas Instruments PLM oder den Silicon Light Machines PLV. Was das technische Potenzial angeht, sticht der RealHolo aus der Masse der MEMS deutlich heraus.
Flüssigkristall auf Silizium - LCoS
Eine weitere beliebte Phasen-SLM-Technologie ist Liquid Crystal on Silicon (LCoS). Diese Mikrodisplays beruhen auf einem recht komplexen Technologiepaket, zu dem eine CMOS-Backplane, eine metallische Pixelschicht, obere und untere Ausrichtungsschichten für den Flüssigkristall, eine Indium-Zinn-Oxid-Schicht (ITO) zur Erzeugung des elektrischen Feldes über dem Flüssigkristall und ein Deckglas zur Aufnahme des ITO gehören. Trotz dieser Komplexität können die Hersteller LCoS-Panels in großen Mengen mit hoher Ausbeute und minimalen Pixelfehlern produzieren.
LCoS-Panels bieten mehrere Vorteile, darunter Robustheit. Sie haben jedoch auch Nachteile, wie die Abhängigkeit von der Polarisation. Außerdem begrenzt die Dicke der Flüssigkristallschicht, die durch die Wellenlänge bestimmt wird, für die das SLM ausgelegt ist, die effektive Auflösung des Modulators. Diese Einschränkung ergibt sich aus der Natur der elektrischen Felder, die dazu neigen, sich von ihrer Quelle auszubreiten. LCoS-Panels bestehen im Wesentlichen aus dicht gepackten transparenten Kondensatoren. Wenn die laterale Größe eines jeden Kondensators kleiner ist als der Abstand zwischen seinen Platten, schwappt das elektrische Feld in benachbarte Pixel über und erzeugt Übersprechen. In der LCoS-Industrie ist dieses Phänomen als Streufeld-Effekt bekannt. Es verursacht sowohl unerwünschte Polarisationseffekte als auch Enthüllungen. Bevor wir uns mit den MEMS-SLMs befassen, müssen wir einen großen Vorteil erwähnen, nämlich dass man sie heute bei Unternehmen wie Hamamatsu oder Holoeye Photonics.
MEMS-Kolben-Spiegel-Arrays
Auch wenn die Kolben-MEMS-Geräte nicht so selten sind wie Einhörner, wird man in freier Wildbahn nicht so leicht eines entdecken. Davon abgesehen, es gibt sie wirklich und wenn Texas Instruments das PLM schließlich auf den Markt bringt, könnten sie tatsächlich recht verbreitet werden. Kolbengeräte sind aus optischer Sicht sehr flexibel. Es gibt keine nennenswerten Polarisationseffekte. Es gibt keine Wellenlängenabhängigkeit, solange wir mit jeweils einer Wellenlänge beleuchten. Sie sind schnell und die Phase ist stabil. Bei LCoS muss man häufig die Polarität der Ansteuerspannung ändern, um eine Verschlechterung des Flüssigkristalls zu verhindern. Das ist hier nicht der Fall. 360-Grad-Phasenmodulation und kein störendes Übersprechen. Großartig. Kann ich ein Bündel haben? Es gibt ein Problem, das auch für LCoS-Panels gilt: Wie entscheiden Sie, welche Phase für jedes beleuchtete Pixel eingestellt werden soll?
Bilderzeugung mit reinen Phasengeräten
Normalerweise greifen wir auf den Gerchberg-Saxton-Algorithmus zurück, wenn wir dieses Problem lösen müssen. Er ist besonders nützlich bei visuellen Anwendungen, wo das Gehirn das Ergebnis schmackhafter macht. Ein großer Vorteil von phasenmodulierenden Geräten ist, dass wir keine Optik benötigen. Beleuchten Sie mit einem ausreichend breiten Lichtstrahl und Sie haben einen Projektor aus zwei Teilen, Lichtquelle und SLM. Die Wellenlänge und die Pixelgröße begrenzen die Winkelausdehnung, aber wenn das ausreicht, sind wir fertig. Andernfalls können wir ein galileisches Teleskop verwenden, um die gewünschte Vergrößerung zu erreichen.
In der Lithografie, wo die Bildqualität alles ist, müssen wir die reflektierte Phase des Lichts kontrollieren. Gelingt uns dies über eine große Entfernung nicht, bewegen sich unsere Objekte durch den Fokus. Gelingt dies nicht über einen kurzen Bereich, werden unsere Objekte mit Flecken versehen, die zudem durch die Aberrationen unserer Projektionsoptik noch verstärkt werden.
Es gibt jedoch noch einen weiteren Punkt zu berücksichtigen. Wie entscheiden wir, welche Phase wir für jedes Pixel festlegen? Die Methoden zum Abrufen der Phase sind iterativ und liefern meines Wissens eine zufällig projizierte Phase. Die direkten Methoden, die ich kenne, verwenden neuronale Netze, aber ich habe nicht gesehen, welche Bildqualität wir von ihnen erwarten können. Ich würde erwarten, dass der Ansatz des neuronalen Netzes bestenfalls die Ergebnisse der zum Training verwendeten Methoden zur Phasenwiederherstellung reproduziert. Folglich würde ich erwarten, dass diese Methoden eine zufällige Phase erzeugen.
Einige theoretische Grundlagen
Bei der Erzeugung von Mustern hoher Qualität mit reinen Phasenmodulatoren müssen wir zumindest zwei Fälle unterscheiden: den linearen Abbildungsfall und den nichtlinearen Fall. Der lineare Abbildungsfall entspricht der linearen Abbildung zwischen Modulator und Bildamplitude bei der kohärenten Bildgebung, während der nichtlineare Fall für die teilkohärente Bildgebung gilt.
Bei der kohärenten Bildgebung wissen wir, dass die Bildamplitude eine lineare "Funktion" der reflektierten Amplitude ist,
Und wenn P ein diskretes Gerät darstellt, können wir das Integral in eine Summe umwandeln, indem wir über die "Pixel" integrieren,
Es gibt Details dazu, die wir im Moment wohl auslassen können. Wir wissen jedoch, dass wir diese Beziehung auf die eine oder andere Weise umkehren können,
Praktisch gesehen ist die Umkehrung von H ist in der Regel eine Pseudo-Inverse und so weiter. Das ist nicht der Punkt. Doch selbst für den einfachen Fall, dass die Impulsantwort H real ist (d. h. kein Imaginärteil) und die zu lösende Amplitude ebenfalls real ist, ergibt sich die Lösung (p) ist dann real. Nicht gerade eine tolle Lösung für ein Kolbengerät.
Kolben brauchen eine Abbildung auf den komplexen Einheitskreis
Wir brauchen also eine Möglichkeit, einen reellen Vektor zu transformieren p (mit NxM Elementen, wobei NxM die Größe unseres SLM ist) in einen Vektor,
wobei der Vektor h hat die gleiche Größe wie p. Wir wollen die Höhen, hdie Eigenschaft zu haben, dass,
Das heißt, wir wollen den imaginären Teil mit Hilfe des optischen Systems aufheben. Es geht mir nicht darum, diesen Blog in eine mathematische Abhandlung zu verwandeln, aber ein gut durchdachtes Bildsystem, das für die Grauskalierung gedacht ist, lässt eine Menge Raum für Lösungen h die den durch das Mapping erzeugten Bildern sehr nahe kommen Hp.
For linear mappings, or coherent systems in other words, there is quite a lot we can do to find a distribution of piston phases, without combining (say) 4 pixels to create an effective gray pixel, which would lead to 4 times writing capacity loss. We would need to dive into lots more math to describe the procuess fully, so maybe another time.
Wenn der Himmel nicht die Grenze ist SLM
Der Kolbenmodulator für die Lithografie ist der ultimative Modulator für alle, die die Auflösung im Sub-Wellenlängenbereich über die sonst üblichen Grenzen hinaus steigern wollen, aber er hat seinen Preis. Hier ist der Punkt. Ein Kolbenmodulator kann jede beliebige Phase und Amplitude (relativ gesehen) projizieren, aber für die Lithografie wollen wir eigentlich keine Amplitude. Wir wollen, dass das Bild eine konstante Phase über das gesamte Bild hat, denn eine Phasenvariation bedeutet eine Variation der Merkmalsabmessungen oder der Platzierung durch den Fokus, und das wollen wir auf keinen Fall. Das bedeutet, dass wir Zeit aufwenden müssen, um eine Lösung zu finden, die diesen speziellen Freiheitsgrad des Modulators einschränkt.
Den Kuchen zu haben und ihn zu essen, Micronic erfand einen Kippspiegel Design, das einen Viertel-Wellenlängenschritt über eine Hälfte des Spiegels beinhaltete. Das Ergebnis war eine Bildamplitude, die einen (relativen) Bereich von -1 bis 1 und eine Phasenvariation von Null erreichen konnte. All die guten Dinge, für die man den Kolbenspiegel brauchte, ohne die Arbeit. Der Nachteil war eine Verringerung des Reflexionsvermögens des Geräts, was bei einer Anwendung mit einem Excimer-Laser kein Problem darstellte. Streng genommen kann es 2D-Topologien geben, die dieser Modulator in einem einzigen Bild nicht bewältigen kann. Dennoch, ASML entschied sich für diese Lösung für sein Direktschreibe-Riesenprodukt. Leider hat ASML dieses Produkt nie veröffentlicht. Meines Wissens ist dies der größte SLM, der bisher entwickelt und hergestellt wurde. 11 Millionen analog gekippte 8-Mikrometer-Spiegel und 6 kHz Bildwiederholrate. Sie können ein schönes Bild finden SEM-Bild davon hier.
Möchten Sie mehr wissen?
Wenn Sie mehr wissen möchten, wenden Sie sich bitte an kontaktieren Sie mich über die Kontaktseite oder senden Sie einfach eine E-Mail an [email protected]. Ich rede gerne über SLMs. Sie können auch gleich hier einen Kommentar hinterlassen.




Kommentar verfassen