Ce billet sera le premier d'une série de trois sur l'application des méthodes graphiques de Goodman et l'illumination partiellement cohérente, avec un accent particulier sur son application aux modulateurs spatiaux de lumière. Cette introduction commencera avant l'article de Goodman et se terminera à peu près là où son article commence. Nous espérons qu'elle servira d'introduction à la terminologie et aux concepts de l'article.
Cohérence partielle - Rien à craindre

Concevoir un système d'imagerie partiellement cohérent, en particulier un système qui implique un modulateur spatial de lumière, peut être une tâche ardue. Les modulateurs spatiaux de lumière sont des systèmes complexes en soi et concevoir un système à partir de zéro, à la merci d'outils de simulation opaques, revient à éclairer une pièce sombre à l'aide d'un pointeur laser. Les choses deviennent assez claires à l'endroit éclairé, mais l'image globale fait toujours défaut.
Le problème de l'imagerie partiellement cohérente est que nous ne pouvons plus nous appuyer sur des concepts familiers tels que la cartographie linéaire. Avec les systèmes d'imagerie incohérents, nous pouvons additionner les intensités. Pour les systèmes d'imagerie cohérents, nous additionnons les amplitudes, mais les systèmes d'imagerie partiellement cohérents sont linéaires dans la fonction de cohérence mutuelle, ce qui n'offre malheureusement que très peu d'informations supplémentaires sur le processus d'imagerie.
Il y a cependant un soulagement offert par Goodman. Non, pas Joseph Goodman. Je parle de Douglas Goodman. L'article de Goodman, "Méthodes graphiques pour aider à comprendre l'imagerie partiellement cohérente"Il s'agit d'un excellent document qui offre des perspectives utiles sur le sujet et qui, à l'aide d'un graphique bidimensionnel, permet de comprendre certains résultats non intuitifs, à la fois quantitatifs et qualitatifs.
L'auteur couvre le sujet de plusieurs points de vue, mais se lance dans l'histoire en supposant que le lecteur est familier avec le formalisme. D'après mon expérience, c'est parfois un pont trop loin pour de nombreux lecteurs. C'est pourquoi cet exposé technique tentera de combler le fossé et servira de préambule à l'article. Puisque ce sujet est déjà rigoureusement couvert dans plusieurs textes standards tels que Born & Wolf ou Statistical Optics de J. Goodman, nous allons passer outre les détails théoriques afin de nous concentrer sur les concepts les plus importants pour le cas particulier de l'imagerie d'un objet unidimensionnel, une ligne.
Retour aux sources
Commençons donc par un sujet avec lequel la plupart des lecteurs sont à l'aise, à savoir le calcul de l'intensité d'une image cohérente d'un objet (O) à travers un système optique caractérisé par la réponse impulsionnelle (H). Les symboles utilisés ici sont les mêmes que dans l'article afin de faciliter le passage à l'article de Goodman pour ceux qui le souhaitent.
Il ne nous reste plus que deux obstacles à franchir pour obtenir la vue d'ensemble qui est notre objectif ici, le premier étant de savoir pourquoi un objet unidimensionnel nécessite une intégrale bidimensionnelle. Celle-ci est simple car elle consiste à étendre l'expression ci-dessus à son amplitude et à son conjugué complexe. Et voilà. Deux intégrales. Avons-nous terminé ? Presque.
Mais c'est l'heure des aveux. La cohérence partielle n'existe pas. La physique quantique nous dit qu'une particule n'interfère qu'avec elle-même ou pas du tout. C'est assez simple, n'est-ce pas ? Lorsque nous mettons en place un système partiellement cohérent, nous avons besoin d'une source incohérente dont l'étendue est suffisante pour éclairer tous les objets que nous voulons faire entrer dans une seule image. Pour le sujet qui nous occupe, nous pouvons oublier l'étendue, mais nous devons considérer la source incohérente à l'infini, ou, en pratique, à l'autre extrémité d'un système 2F collimaté.
Cela signifie-t-il que nous pouvons simplement additionner les intensités de toutes les ondes planes provenant de la source ?
Non, car l'intégrale ci-dessus ne tient pas correctement compte de l'éclairage hors axe. Notre réponse impulsionnelle (H) ne se préoccupe pas de la direction de la lumière car une source ponctuelle rayonne dans la demi-sphère, qu'elle soit éclairée de côté ou de face. Cependant, pour décrire l'objet étendu (O), nous devons tenir compte de la variation de la phase impliquée par l'éclairage hors axe. Par conséquent, l'intégrale cohérente de base (par point source) doit être développée,
Nous avons maintenant trois intégrales au lieu des deux promises. Nous nous en occupons en rassemblant tous les termes qui dépendent de la direction incidente et en comprimant le tout dans ce que nous appellerons la fonction de cohérence mutuelle (J),
Enfin, en rassemblant tous les éléments ci-dessus, nous obtenons notre expression finale pour le cas 1D d'une image partiellement cohérente,
De nombreux détails ont été omis pour ne pas perdre de vue l'essentiel, et l'essentiel dans ce cas est (1) que nous avons étendu l'intensité à une amplitude et à son conjugué complexe et (2) que nous avons fait un incohérent la somme des intensités dans (1). Dans ce processus, nous avons réussi à isoler une transformée de Fourier sur la distribution de la densité spectrale (dans l'espace réciproque) de la source incohérente.
En examinant l'expression de J(), l'ingénieur électricien peut penser au théorème de Wiener-Khinchin qui relie la transformée de Fourier d'une densité spectrale à une autocorrélation. En optique, la même mathématique est appelée théorème de Van Citert-Zernike. Les mathématiques sont les mêmes, mais l'intégrale se fait dans l'espace réciproque.
La vue graphique
Maintenant que l'on sait pourquoi le formalisme est tel qu'il est, il est temps de faire le lien avec l'article de Goodman.
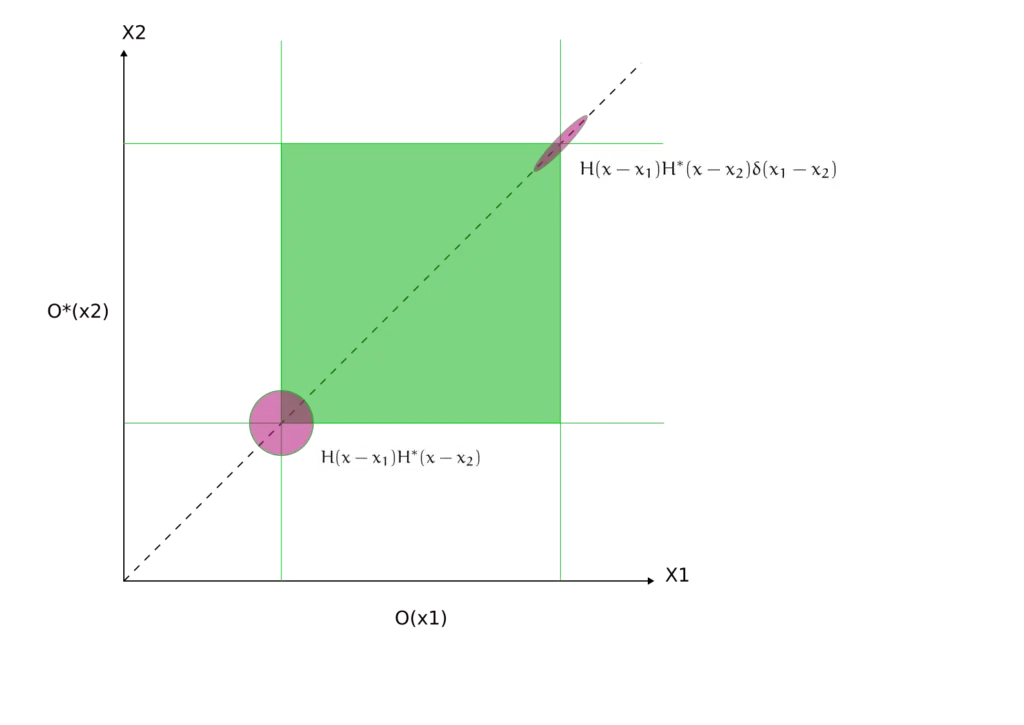
La figure représentée illustre simultanément deux cas d'imagerie distincts : l'imagerie cohérente en bas à gauche et l'imagerie incohérente en haut à droite. Les formes magenta dans le graphique tentent d'encapsuler la symétrie de l'intégrande. Dans l'article de Goodman, il s'agit de la "fonction de projection", qui émerge du produit de la réponse impulsionnelle et de la fonction de cohérence.
Lorsque la source lumineuse couvre un grand angle solide, la fonction de cohérence subit une annulation significative au sein de son intégrale. Par conséquent, les valeurs non nulles de la fonction de cohérence se trouvent principalement près de la diagonale. En revanche, pour un éclairage cohérent, la fonction de cohérence conserve une valeur constante sur l'ensemble du plan. Cette constance est symbolisée sur la figure par un cercle, qui souligne les propriétés de symétrie de la fonction de projection, notée HH*.
Quels enseignements pouvons-nous donc tirer de cette visualisation ? L'intensité, I(x), résulte de la convolution de la fonction de projection avec l'objet - représenté par un carré - le long de la diagonale où x1 est égal à x2. Une observation directe est que, dans l'imagerie cohérente, la valeur de I(x) au bord de l'objet ne représente qu'un quart de sa valeur à l'intérieur de l'objet. Cela implique que pour qu'un objet soit efficacement exposé en utilisant l'illumination cohérente, la dose nécessaire pour une réserve à fort contraste est quadruple de la dose nécessaire pour l'éclaircir.
Inversement, pour l'imagerie incohérente représentée en haut à droite, la dose d'exposition correcte pour l'imagerie incohérente est le double de la dose pour éclaircir. Cela s'explique par le fait que la moitié de la fonction de projection se trouve à l'intérieur de l'objet, tandis que l'autre moitié se trouve à l'extérieur, comme l'illustrent les produits O(x1)O*(x2).
Ces interprétations sont les résultats les plus apparents de la méthode graphique de Goodman, mais il en existe une myriade d'autres, qui feront l'objet des prochains Tech Talks. Bien que les principales applications de cette méthode soient ancrées dans la lithographie, elle trouve parfois sa place dans l'interférométrie.
Notre prochain article de blog examinera comment les propriétés d'imagerie sont influencées par les imperfections ou les caractéristiques intentionnellement incorporées de divers modulateurs spatiaux de lumière. Restez informé en vous inscrivant sur notre page de contact.



Laisser un commentaire